题目内容
设数列{an}的首项a1=-9，且满足an+1=an+2，则|a1|+|a2|+…+|a20|= ．
考点：数列的求和,等差数列的前n项和,数列递推式
专题：等差数列与等比数列
分析：由已知条件推导出{an}是首项为-9，公差为2的等差数列，由此能求出|a1|+|a2|+…+|a20|的值．
解答：
解：∵数列{an}的首项a1=-9，且满足an+1=an+2，
∴{an}是首项为-9，公差为2的等差数列，
∴an=-9+（n-1）×2=2n-11，
由an=2n-11≥0，得n≥
，
a5=2×5-11=-1，a6=2×6-11=1，
∴|a1|+|a2|+…+|a20|=S20-2S5
=20×（-9）+
×2-2[5×（-9）+
×2]
=250．
故答案为：250．
∴{an}是首项为-9，公差为2的等差数列，
∴an=-9+（n-1）×2=2n-11，
由an=2n-11≥0，得n≥
| 11 |
| 2 |
a5=2×5-11=-1，a6=2×6-11=1，
∴|a1|+|a2|+…+|a20|=S20-2S5
=20×（-9）+
| 20×19 |
| 2 |
| 5×4 |
| 2 |
=250．
故答案为：250．
点评：本题考查数列的前20项的绝对值的和的求法，是中档题，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
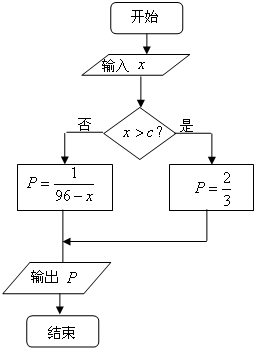某厂生产一种仪器，由于受生产能力与技术水平的限制，会产生一些次品．根据经验知道，该厂生产这种仪器，次品率p与日产量x（件）（x∈N*）之间大体满足如框图所示的关系（注：次品率P=已知
=（2，-1，3），
=（-1，4，-2），
=（4，5，x），若
、
、
三向量共面，则|
|=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| A、5 | ||
| B、6 | ||
C、
| ||
D、
|