题目内容
10.直线y=-x+2与圆x2+y2=3相交于A、B两点,则线段AB的长是2.分析 圆x2+y2=3的圆心O(0,0),半径r=$\sqrt{3}$,先求出圆心O(0,0)到直线y=-x+2的距离d,再由线段AB的长|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$,能求出结果.
解答 解:圆x2+y2=3的圆心O(0,0),半径r=$\sqrt{3}$,
圆心O(0,0)到直线y=-x+2的距离d=$\frac{|0+0-2|}{\sqrt{2}}$=$\sqrt{2}$,
∴线段AB的长|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{3-2}$=2.
故答案为:2.
点评 本题考查圆的弦长的求法,涉及到圆、直线方程、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
1.a,b是正实数,且a+b=4,则有( )
| A. | $\frac{1}{ab}$≥$\frac{1}{2}$ | B. | $\frac{1}{a}$+$\frac{1}{b}$≥1 | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{{a}^{2}+{b}^{2}}$≥$\frac{1}{4}$ |
15.已知f(x)=ax2+bx,其中-1≤a<0,b>0,则“存在x∈[0,1],|f(x)|>1”是“a+b>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数y=sinx的图象与函数y=x图象的交点的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.已知三棱锥A-BCD四个顶点都在半径为3的球面上,且BC过球心,当三棱锥A-BCD的体积最大时,则三棱锥A-BCD的表面积为( )
| A. | $18+6\sqrt{3}$ | B. | $18+8\sqrt{3}$ | C. | $18+9\sqrt{3}$ | D. | $18+10\sqrt{3}$ |

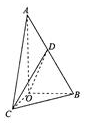 如图所示,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.
如图所示,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.