题目内容
5.已知函数f(x)=(1+$\frac{1}{tanx}$)sin2x-2sin(x+$\frac{π}{4}$)sin(x-$\frac{π}{4}$).(1)用五点法画出它在一个周期内的闭区间上的图象,并写出f(x)的周期、振幅、初相;
(2)若x∈[$\frac{π}{12}$,$\frac{π}{2}$],求f(x)的取值范围.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)$+\frac{1}{2}$,可求f(x)的周期,振幅,初相,列表,描点,连线,用五点法即可画出它在一个周期内的闭区间上的图象.
(2)由x∈[$\frac{π}{12}$,$\frac{π}{2}$],可求2x+$\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{5π}{4}$],利用正弦函数的图象和性质即可得解f(x)的取值范围.
解答 解:(1)∵f(x)=(1+$\frac{1}{tanx}$)sin2x-2sin(x+$\frac{π}{4}$)sin(x-$\frac{π}{4}$)
=sinx(sinx+cosx)-2($\frac{\sqrt{2}}{2}$sinx+$\frac{\sqrt{2}}{2}$cosx)($\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx)
=sinxcosx+cos2x
=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)$+\frac{1}{2}$.
∴f(x)的周期T=$\frac{2π}{2}=π$、振幅为$\frac{\sqrt{2}}{2}$、初相为$\frac{π}{4}$;
列表可得:
| 2x+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ |
| sin(2x+$\frac{π}{4}$) | 0 | 1 | 0 | -1 | 0 |
| y | $\frac{1}{2}$ | $\frac{3}{2}$ | $\frac{1}{2}$ | -$\frac{1}{2}$ | $\frac{1}{2}$ |
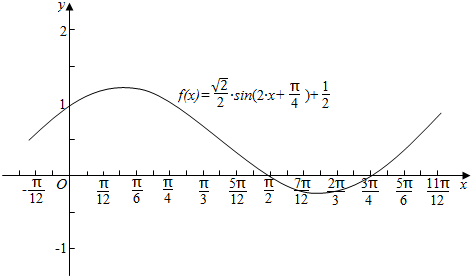 --------(4分)
--------(4分)(2)∵x∈[$\frac{π}{12}$,$\frac{π}{2}$],
∴2x+$\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{5π}{4}$],
∴sin(2x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],
∴f(x)=$\frac{\sqrt{2}}{2}$sin(2x+$\frac{π}{4}$)$+\frac{1}{2}$∈[0,$\frac{\sqrt{2}+1}{2}$].
点评 本题主要考查了五点法作函数y=Asin(ωx+φ)的图象,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
15.已知变量x,y满足约束条件$\left\{\begin{array}{l}{y-3x+1≤0}\\{y-x+1≥0}\\{y≤0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 4 | B. | 2 | C. | 1 | D. | -4 |
16.关于x的方程x2-2x+lg(2a2-a)=0有一个正根和一个负根的充分不必要条件是( )
| A. | -$\frac{1}{2}$<a<1 | B. | -$\frac{1}{2}$<a<0 | C. | 0<a<1 | D. | -$\frac{1}{2}$<a<0或$\frac{1}{2}$<a<1 |
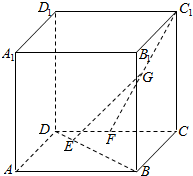 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点E在线段BD上且|DE|=$\frac{1}{3}$|EB|,点F是CD的中点,G为C1F的中点,求EG的长.



