题目内容
15.y=2sinωx与y=2cosωx(ω>0)的图象的交点中,相邻的两个交点的距离为2$\sqrt{3}$,则ω=$\frac{π}{2}$.分析 由题意利用勾股定理可得2$\sqrt{3}$=$\sqrt{{(\frac{π}{ω})}^{2}{+(\sqrt{2}+\sqrt{2})}^{2}}$,由此求得ω 的值.
解答 解:由题意可得$\frac{T}{2}$=$\frac{π}{ω}$,2$\sqrt{3}$=$\sqrt{{(\frac{π}{ω})}^{2}{+(\sqrt{2}+\sqrt{2})}^{2}}$,∴ω=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题主要考查正弦函数、余弦函数的周期性和图象特征,勾股定理的应用,属于基础题.

练习册系列答案
相关题目
6.已知集合A={1,2,5},集合B={2,3,4},全集U={0,1,2,3,4,5},则∁UA∪B=( )
| A. | {0,1,2,3,4} | B. | {0,2,3,4} | C. | {3,4} | D. | {0,3,4| |
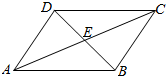 如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.
如图,在平行四边形ABCD中,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+y$\overrightarrow{AB}$,则x+y=1.