题目内容
10.函数g(x)=sinx•log2($\sqrt{{x}^{2}+t}$+x)为偶函数,则t=1.分析 根据函数奇偶性的定义建立方程关系进行求解即可.
解答 解:∵g(x)=sinx•log2($\sqrt{{x}^{2}+t}$+x)为偶函数,
∴g(-x)=g(x),
即-sinx•log2($\sqrt{{x}^{2}+t}$-x)=sinx•log2($\sqrt{{x}^{2}+t}$+x),
即log2($\sqrt{{x}^{2}+t}$-x)=-log2($\sqrt{{x}^{2}+t}$+x),
则log2($\sqrt{{x}^{2}+t}$-x)+log2($\sqrt{{x}^{2}+t}$+x)=0,
即log2($\sqrt{{x}^{2}+t}$-x)($\sqrt{{x}^{2}+t}$+x)=log2(x2+t-x2)=log2t=0,
即t=1,
故答案为:1.
点评 本题主要考查函数奇偶性的应用,根据定义建立方程关系,结合对数的运算法则是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.“α≠β”是“cosα≠cosβ”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
1.设p、q是两个命题.如果命题p是命题q的充分不必要条件.那么¬p是¬q的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
18.汽车发动机排量可以分为两大类,高于1.6L的称为大排量,否则称为小排量,加油时,有92号与95号两种汽油可供选择,某汽车相关网站的注册会员中,有300名会员参与了网络调查,结果如下:
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅰ)根据此次调查,是否有95%的把握认为该网站会员给汽车加油时进行的型号选择与汽车排量有关?
(Ⅱ)从调查的大排量汽车中按“加油类型”用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个整体,从中任取抽取3辆汽车,求这3辆汽车都是“加92号汽油”的概率.
| 汽车排量 加油类型 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
| P(K2)≥k | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(Ⅱ)从调查的大排量汽车中按“加油类型”用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个整体,从中任取抽取3辆汽车,求这3辆汽车都是“加92号汽油”的概率.
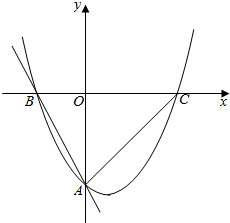 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点