已知两条直线l1:x+(1+m)y=2-m.l2:2mx+4y=-16．m为何值时.l1与l2:(1)相交,(2)平行．题目和参考答案——青夏教育精英家教网——

题目内容

19．已知两条直线l₁：x+（1+m）y=2-m，l₂：2mx+4y=-16．m为何值时，l₁与l₂：
（1）相交；
（2）平行．

分析（1）利用两条直线相交时，由方程组得到的一次方程有唯一解，一次项的系数不等于0．
（2）利用两直线平行时，一次项系数之比相等，但不等于常数项之比，求出m的值．

解答解：（1）当L₁与L₂相交时⇒4≠2m（1+m）⇒m≠1且m≠-2；
（2）当L₁与L₂平行时⇒4=2m（1+m）⇒m=1或m=-2；
经检验m=-2时，两直线重合，所以，m=1．

点评本题考查两直线相交、重合、平行的条件，体现了转化的数学思想．

练习册系列答案

快乐练练吧同步练习系列答案

中学生世界系列答案

同步课时练测卷系列答案

孟建平小学滚动测试系列答案

口算题卡西安出版社系列答案

黄冈360度口算应用题卡系列答案

希望考苑能力测评卷系列答案

名师金卷系列答案

课堂作业武汉出版社系列答案

黄冈天天练口算题卡系列答案

相关题目

9．已知向量$\overrightarrow{a}$=（-2，-1），$\overrightarrow{a}$•$\overrightarrow{b}$=10，|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5}$，则|$\overrightarrow{b}$|=2$\sqrt{5}$．

10．函数g（x）=sinx•log₂（$\sqrt{{x}^{2}+t}$+x）为偶函数，则t=1．

7．下列命题错误的是（　　）

	A．	如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
	B．	如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β
	C．	如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥平面γ
	D．	如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β

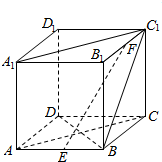已知ABCD-A₁B₁C₁D₁为正方体，E、F分别是AB、B₁C₁的中点．
（1）求证：直线EF∥平面ACC₁A₁；
（2）求直线BC₁与平面ACC₁A₁所成角的余弦值．

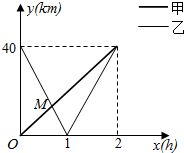在一条笔直公路上有A，B两地，甲骑自行车从A地到B地，乙骑着摩托车从B地到A地，到达A地后立即按原路返回，如图是甲乙两人离A地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）直接写出y_甲，y_乙与x之间的函数关系式（不必写过程），求出点M的坐标，并解释该点坐标所表示的实际意义；
（2）若两人之间的距离不超过5km时，能够用无线对讲机保持联系，求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系；
（3）若甲乙两人离A地的距离之积为f（x），求出函数f（x）的表达式，并求出它的最大值．

11．已知圆O₁：x²+y²-4x+4y-41=0，圆O₂：（x+1）²+（y-2）²=4，则两圆的位置关系为（　　）

8．设函数y=4^x-3•2^x+3的值域为[1，7]，若定义域为（-∞，0]∪[a，2]，求实数a的取值范围．

9．已知a＞0，b＞0，且a+b=2．
（1）求a•b的最大值；
（2）求$\frac{1}{a}+\frac{4}{b}$的最小值．