题目内容
2.观察以下各式:cos6°cos54°cos66°=$\frac{1}{4}$cos18°,cos19°cos41°cos79°=$\frac{1}{4}$cos57°,cos27°cos33°cos87°=$\frac{1}{4}$cos81°.(1)分析上述各式的共同特点,写出一个能反映一般规律的等式;
(2)证明你写出的等式.
分析 (1)利用条件,可得一般规律的等式;
(2)利用和差的余弦公式,结合二倍角公式证明等式.
解答 解:(1)由题意,cosαcos(60°-α)cos(60°+α)=$\frac{1}{4}$cos3α.
(2)左边=cosα($\frac{1}{2}$cosα+$\frac{\sqrt{3}}{2}$sinα)($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα)=$\frac{1}{4}cosα$(cos2α-$\frac{3}{4}$sin2α)
右边=$\frac{1}{4}cosα$cos2α+$\frac{1}{4}$sinαsin2α=$\frac{1}{4}cosα$(cos2α-sin2α+$\frac{1}{4}$sin2α)=$\frac{1}{4}cosα$(cos2α-$\frac{3}{4}$sin2α).
∴cosαcos(60°-α)cos(60°+α)=$\frac{1}{4}$cos3α.
点评 本题考查类比推理,考查对于所给的式子的理解,从所给式子出发,通过观察、类比、猜想出一般规律,着重考查了类比的能力.

练习册系列答案
相关题目
12.设m,n∈(0,+∞),若直线(m+2)x+(n+2)y-4=0与圆(x-1)2+(y-1)2=1相切,则m+n的最小值是( )
| A. | 4+4$\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | 4+$\sqrt{2}$ | D. | 4+2$\sqrt{2}$ |
13.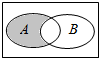 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
 已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )
已知全集I={1,2,3,4,5,6},集合A={3,4,5},B={1,5,6},则图中阴影部分表示的集合是( )| A. | {2,3,4} | B. | {2,3,4,5} | C. | {3,4} | D. | {3,4,5} |
17.设命题p:?n∈N,n2>2n,则¬p为( )
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |
7.下列命题错误的是( )
| A. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
11.已知圆O1:x2+y2-4x+4y-41=0,圆O2:(x+1)2+(y-2)2=4,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
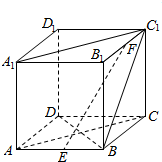 已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.
已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.