题目内容
15.在平面直角坐标系xOy中,已知向量$\overrightarrow{m}$=($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{n}$=(sinx,cosx),x∈(0,$\frac{π}{2}$).(1)若$\overrightarrow{m}$⊥$\overrightarrow{n}$,求tanx的值;
(2)若$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$,求sinx+cosx的值.
分析 (1)根据向量垂直的性质得到坐标的关系等式,求出tanx;
(2)利用数量积公式得到x的三角函数等式,结合平方关系求出sinx+cosx.
解答 解:(1)因$\overrightarrow{m}$⊥$\overrightarrow{n}$,所以$\frac{{\sqrt{2}}}{2}$sinx-$\frac{{\sqrt{2}}}{2}$cosx=0 …(2分)
所以tanx=1 …(5分)
(2)因为$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$,$\overrightarrow m•\overrightarrow n=\frac{{\sqrt{2}}}{2}sinx-\frac{{\sqrt{2}}}{2}cosx=\frac{1}{2}$,所以$sinx-cosx=\frac{{\sqrt{2}}}{2}$①…(7分)
设sinx+cosx=a②
由①2+②2得a2=$\frac{3}{2}$ …(10分)
因x是锐角,所以a为正值,所以a=$\frac{{\sqrt{6}}}{2}$…(12分)
点评 本题考查了平面向量的坐标运算以及向量垂直的性质和三角函数的化简求值;属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.从2名男生和2名女生选出2名参加某项活动,则选出的2名学生中至少有1名女生的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{4}$ |
7.下列命题错误的是( )
| A. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
 已知函数f(x)=|x-1|+|x+1|(x∈R)
已知函数f(x)=|x-1|+|x+1|(x∈R)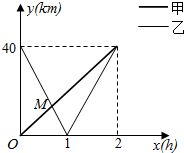 在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: