题目内容
定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[-2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2-mx-1是[-1,1]上的“平均值函数”,则实数m的取值范围是 .
| f(b)-f(a) |
| b-a |
考点:函数的概念及其构成要素
专题:函数的性质及应用
分析:函数f(x)=x2-mx-1是区间[-1,1]上的平均值函数,故有x2-mx-1=
在(-1,1)内有实数根,求出方程的根,让其在(-1,1)内,即可求出实数m的取值范围.
| f(1)-f(-1) |
| 1-(-1) |
解答:
解:∵函数f(x)=x2-mx-1是区间[-1,1]上的平均值函数,
∴关于x的方程x2-mx-1=
在(-1,1)内有实数根.
即x2-mx-1=-m在(-1,1)内有实数根.
即x2-mx+m-1=0,解得x=m-1,x=1.
又1∉(-1,1)
∴x=m-1必为均值点,
即-1<m-1<1⇒0<m<2.
∴所求实数m的取值范围是(0,2).
故答案为:(0,2)
∴关于x的方程x2-mx-1=
| f(1)-f(-1) |
| 1-(-1) |
即x2-mx-1=-m在(-1,1)内有实数根.
即x2-mx+m-1=0,解得x=m-1,x=1.
又1∉(-1,1)
∴x=m-1必为均值点,
即-1<m-1<1⇒0<m<2.
∴所求实数m的取值范围是(0,2).
故答案为:(0,2)
点评:本题主要是在新定义下考查二次方程根的问题.在做关于新定义的题目时,一定要先认真的研究定义理解定义,再按定义做题.

练习册系列答案
相关题目
已知集合M={x|-2<x<3},N={x|2x+1≥1},则M∩N等于( )
| A、(-2,-1] |
| B、(-2,1] |
| C、[1,3) |
| D、[-1,3) |
已知正方体的棱长为2
,则其外接球的表面积为( )
| 3 |
| A、48π | B、36π |
| C、32π | D、12π |
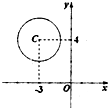 已知圆C:(x+3)2+(y-4)2=4
已知圆C:(x+3)2+(y-4)2=4