题目内容
15.已知集合A={x|2x2-7x+3≤0},集合B={x|x2-a<0,a∈R}.(1)若a=4,求A∩B和A∪B.
(2)若A∩B=∅,求实数a的取值范围.
分析 (1)化简集合A,B,即可求A∩B和A∪B.
(2)若A∩B=∅,分类讨论,即可求实数a的取值范围.
解答 解:(1)∵A={x|2x2-7x+3≥0}={x|(2x-1)(x-3)≥0}={x|x≥3,或x≤$\frac{1}{2}$},
当a=4时,B={x|x2-4<0}={x|-2<x<2},
∴A∩B={x|-2<x≤$\frac{1}{2}$},A∪B={x|x<2,或 x≥3}.
(2)当a≤0时,B=∅,满足A∩B=∅;
当a>0时,B={x|x2-a<0}={x|-$\sqrt{a}$<x<$\sqrt{a}$ },
由A∩B=∅,可得$\sqrt{a}$≤$\frac{1}{2}$,解得 a≤$\frac{1}{4}$.
综上可得,a≤$\frac{1}{4}$,即实数a的取值范围为(-∞,$\frac{1}{4}$].
点评 本题考查集合的化简与运算,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
6.设锐角α终边上一点P的坐标是(3cosθ,sinθ),则函数y=θ-α(0<θ<$\frac{π}{2}$)的最大值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
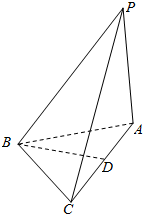 如图,三棱锥P-ABC中,PA⊥平面ABC,AB=BC,AC=2$\sqrt{2}$,PA=2,D是AC的中点
如图,三棱锥P-ABC中,PA⊥平面ABC,AB=BC,AC=2$\sqrt{2}$,PA=2,D是AC的中点