题目内容
3.已知函数f(x)=$\frac{1}{3}{x}^{3}-ax+4,(a>0)$(1)讨论函数 f (x)的单调性;
(2)若对任意的a∈[1,4),都存在x0∈(2,3]使得不等式f(x0)+ea+2a>m成立,求实数m 的取值范围.
分析 (1)求函数的导数,利用函数单调性和导数之间的关系进行求解即可.
(2)求函数的最值,利用参数分离法进行求解即可.
解答 解:(1)f′(x)=x2-a=(x-$\sqrt{a}$)(x+$\sqrt{a}$),
由f′(x)>0得x>$\sqrt{a}$或x<-$\sqrt{a}$,此时函数单调递增,即函数的单调递增区间为(-∞,-$\sqrt{a}$]∪[$\sqrt{a}$,+∞),
由f′(x)<0得-$\sqrt{a}$<x<$\sqrt{a}$,此时函数单调递减,即函数的单调递减区间为[-$\sqrt{a}$,$\sqrt{a}$].
(2)∵a∈[1,4),∴$\sqrt{a}$∈[1,2),
由(1)知,f(x)在(2,3]上单调递减,∴当x∈[2,3)时,函数f(x)的最大值为f(3)=13-3a,
若任意的a∈[1,4),都存在x0∈(2,3]使得不等式f(x0)+ea+2a>m成立,
等价为不等式13-3a+ea+2a>m成立,
即ea-a+13>m,
设g(a)=ea-a+13,a∈[1,4),
此时g′(a)=ea-1≥e-1>0,
∴当a∈[1,4)时,g(a)>g(1)=e+12,
故m≤e+12.
点评 本题主要考查函数单调性的判断以及利用导数研究函数的最值,考查学生的运算和推理能力.

练习册系列答案
相关题目
11.平面α与平面β平行的条件可以是( )
| A. | α内有无穷多条直线都与β平行 | B. | 直线a∥α,a∥β且a?α,a?β | ||
| C. | 直线a?α,b?β且a∥β,b∥α | D. | α内的任意直线都与β平行 |
15.已知全集U=R,集合A={x|y=$\sqrt{2-x}$},B={x|${2}^{-{x}^{2}+3x}$>1},则(∁UA)∩B=( )
| A. | {x|2≤x<3} | B. | {x|2<x<3} | C. | {x|x≥3} | D. | {x|2<x≤3} |
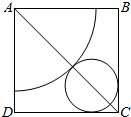 在边长为a的正方形ABCD中,剪下一个扇形和一个圆,如图所示,分别作为圆锥的侧面和底面,求所围成的圆锥的体积.
在边长为a的正方形ABCD中,剪下一个扇形和一个圆,如图所示,分别作为圆锥的侧面和底面,求所围成的圆锥的体积.