题目内容
已知函数f(x)=x2-cosx,对于[-π,π]上的任意x1,x2,有如下条件:
①x1>x2;
②x12>x22;
③|x1|>x2;
④x1>|x2|.
其中能使f(x1)>f(x2)恒成立的条件是 .(写出所有序号)
①x1>x2;
②x12>x22;
③|x1|>x2;
④x1>|x2|.
其中能使f(x1)>f(x2)恒成立的条件是
考点:利用导数求闭区间上函数的最值
专题:函数的性质及应用
分析:当x21>x22时,有|x1|>|x2|,在区间[0,
]内,有
≥x1>x2≥0,f(x1)>f(x2),在区间[-
,0]内,f(x1)>f(x2),从而在区间[-
,
]内恒有f(x1)>f(x2);由函数f(x)=x2-cosx是偶函数,由函数的对称性知离原点越近值越小,由此得x1>|x2|时恒有f(x1)>f(x2).
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:
解:此题最好用数形结合的方法求解.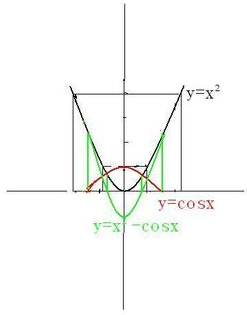
当x21>x22时,有|x1|>|x2|;
故在区间[0,
]内,有
≥x1>x2≥0,
由图中绿线可见:f(x1)>f(x2),
在区间[-
,0]内,有-x1>-x2,
即有-
≤x1<x2≤0,
仍由图中绿线可见:f(x1)>f(x2)
故在区间[-
,
]内恒有f(x1)>f(x2).
由函数f(x)=x2-cosx是偶函数,
由函数的对称性知离原点越近值越小,
∴x1>|x2|时恒有f(x1)>f(x2).
故答案为:②④.

当x21>x22时,有|x1|>|x2|;
故在区间[0,
| π |
| 2 |
| π |
| 2 |
由图中绿线可见:f(x1)>f(x2),
在区间[-
| π |
| 2 |
即有-
| π |
| 2 |
仍由图中绿线可见:f(x1)>f(x2)
故在区间[-
| π |
| 2 |
| π |
| 2 |
由函数f(x)=x2-cosx是偶函数,
由函数的对称性知离原点越近值越小,
∴x1>|x2|时恒有f(x1)>f(x2).
故答案为:②④.
点评:本题主要考查函数与导数等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、数形结合思想、函数与方程思想、化归与转化思想等.

练习册系列答案
相关题目
若M为△ABC所在平面内一点,且满足(
-
)•(
+
-2
)=0,则△ABC的形状为( )
. |
| MB |
. |
| MC |
. |
| MB |
. |
| MC |
. |
| MA |
| A、等腰三角形 |
| B、直角三角形 |
| C、正三角形 |
| D、等腰直角三角形 |
方程x2=cosx的实根的个数是( )
| A、0 | B、1 | C、2 | D、3 |