题目内容
复数
的共轭复数是（ ）
| 1+2i |
| i |
| A、2+i | B、1+2i |
| C、2-i | D、-2+i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用两个复数代数形式的乘法，虚数单位i的幂运算性质求得所给的复数即1+i，从而求得它的共轭复数．
解答：
解：复数
=
=
=2-i，
故它的共轭复数为2+i，
故选：A．
| 1+2i |
| i |
| (1+2i)i |
| i•i |
| -2+i |
| -1 |
故它的共轭复数为2+i，
故选：A．
点评：本题主要考查复数的基本概念，两个复数代数形式的乘法，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
相关题目
设O为△ABC内部的一点，且
+
+2
=0，则△AOC的面积与△BOC的面积之比为（ ）
| OA |
| OB |
| OC |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
设变量x，y满足
，若目标函数z=x-y+1的最小值为0，则m的值为（ ）
|
| A、4 | B、5 | C、6 | D、7 |
已知向量
=（1，2），
=（2，-1），下列结论中不正确的是（ ）
| a |
| b |
A、|
| ||||||||
B、
| ||||||||
C、|
| ||||||||
D、
|
在△ABC中，∠A＜30°是cosA＞
的（ ）
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设曲线C的参数方程为
（t为参数），若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为（ ）
|
| A、sinθ=ρcos2θ |
| B、sinθ=ρcosθ |
| C、2sinθ=ρcos2θ |
| D、sinθ=2ρcos2θ |
一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
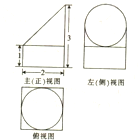
A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |
在实数范围内，不等式||x-2|-1|≤1的解集为（ ）
| A、（0，4] |
| B、[0，4） |
| C、[0，4] |
| D、[1，4] |
如图，在底面为菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=1，PB=PD=