题目内容
已知函数f(x)=2|x|-1(x∈[-1,1]).
(1)作出f(x)的图象;
(2)判断f(x)的奇偶性;
(3)求f(x)的单调区间.
(1)作出f(x)的图象;
(2)判断f(x)的奇偶性;
(3)求f(x)的单调区间.
考点:函数的图象,函数奇偶性的判断
专题:函数的性质及应用
分析:(1)将函数进行化简,即可作出函数图象
(2)根据函数的奇偶性的定义或图象特点即可判断函数的奇偶性.
(3)若x∈[-1,1],根据函数的单调性和图象即可求函数的单调区间.
(2)根据函数的奇偶性的定义或图象特点即可判断函数的奇偶性.
(3)若x∈[-1,1],根据函数的单调性和图象即可求函数的单调区间.
解答:
解:(1)函数f(x)=2|x|-1=
,图象为:
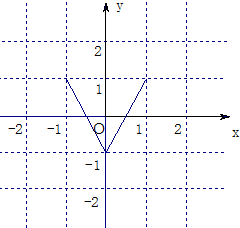
2)由函数f(x)的图象可知,图象关于y轴对称,所以f(x)是偶函数;
3)观察函数f(x)的图象可知,
当x∈[0,1]时,f(x)递增,当x∈[-1,0)时,f(x)递减,
所以f(x)的增区间为[0,1],减区间为[-1,0).
|
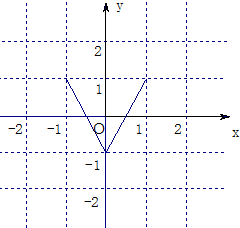
2)由函数f(x)的图象可知,图象关于y轴对称,所以f(x)是偶函数;
3)观察函数f(x)的图象可知,
当x∈[0,1]时,f(x)递增,当x∈[-1,0)时,f(x)递减,
所以f(x)的增区间为[0,1],减区间为[-1,0).
点评:本题主要考查函数图象的做法,以及函数奇偶性和单调性的判断和应用,要求熟练掌握相应的定义,比较基础.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
设Sn是等差数列{an}的前n项和,且S1,S2,S4成等比数列,则
等于( )
| a2 |
| a1 |
| A、1 | B、1或2 | C、1或3 | D、3 |
若函数f(x)=|x|(x-a),a∈R是奇函数,则f(2)的值为( )
| A、2 | B、4 | C、-2 | D、-4 |
若函数y=
的图象关于原点对称,则实数a等于( )
| 4x+a |
| 2x |
| A、-2 | B、-1 | C、1 | D、2 |
已知集合A={0,1,2,4},B={-1,0,1,3},则A∩B=( )
| A、{-1,0,1,2,3,4} |
| B、{0,1} |
| C、{-1,2,3,4} |
| D、{0,1,2} |
