题目内容
函数在f（x）=sinx-ax∈[
，π]上有2个零点，则实数a的取值范围（ ）
| π |
| 3 |
A、[
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
考点：函数的零点与方程根的关系
专题：计算题,作图题,函数的性质及应用
分析：函数在f（x）=sinx-a，x∈[
，π]上有2个零点可化为函数y=sinx与y=a在[
，π]上有两个交点，从而作图求解．
| π |
| 3 |
| π |
| 3 |
解答：
解：函数在f（x）=sinx-a，x∈[
，π]上有2个零点可化为
函数y=sinx与y=a在[
，π]上有两个交点，
作函数y=sinx与y=a在[
，π]上的图象如下，
故a∈[
，1），
故选A．
| π |
| 3 |
函数y=sinx与y=a在[
| π |
| 3 |
作函数y=sinx与y=a在[
| π |
| 3 |
故a∈[
| ||
| 2 |
故选A．
点评：本题考查了函数零点与函数图象的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
在如图的各图中，每个图的两个变量具有线性相关关系的图是（ ）
| A、①② | B、①③ | C、②④ | D、②③ |
向量
=（1，m），
=（2，-4），若
=λ
（λ为实数），则m的值为（ ）
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
函数f（x）=
，若f（2）+f（α）=e+1，则α的所有可能值为（ ）
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|
有一批数量很大的产品，其中次品率为3%，从中任取产品进行不放回抽查，若取到正品则停止；若取到次品则继续，最多取3次．设X表示取出产品的个数，则P（X=3）=（ ）
| A、0.03×0.97 |
| B、0.972×0.03 |
| C、0.032×0.97+0.033 |
| D、0.972×0.03+0.033 |
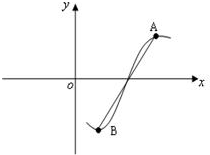函数f（x）=cos（ωx+φ）（ω＞0，0＜φ＜π）为R上的奇函数，该函数的部分图象如图所表示，A，B分别为最高点与最低点，并且两点间的距离为2