题目内容
有一批数量很大的产品，其中次品率为3%，从中任取产品进行不放回抽查，若取到正品则停止；若取到次品则继续，最多取3次．设X表示取出产品的个数，则P（X=3）=（ ）
| A、0.03×0.97 |
| B、0.972×0.03 |
| C、0.032×0.97+0.033 |
| D、0.972×0.03+0.033 |
考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题：概率与统计
分析：X=3 表示取出的产品数为3件，可能是第三次取得正品，也可能第三次仍没有取得正品，分类讨论，利用互独立事件的概率乘法公式求得结果．
解答：
解：由题意可得正品率为0.97，X=3 表示取出的产品数为3件，可能是第三次取得正品，也可能第三次仍没有取得正品，
故P（X=3）=0.032×0.97+0.033，
故选：C．
故P（X=3）=0.032×0.97+0.033，
故选：C．
点评：本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数在f（x）=sinx-ax∈[
，π]上有2个零点，则实数a的取值范围（ ）
| π |
| 3 |
A、[
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
定义在（-1，1）上的函数f（x）-f（y）=f（
），当x∈（-1，0）时，f（x）＞0，若P=f（
）+f（
），Q=f（
），R=f（-
），则P，Q，R的大小关系为 （ ）
| x-y |
| 1-xy |
| 1 |
| 3 |
| 1 |
| 17 |
| 1 |
| 5 |
| 1 |
| 3 |
| A、R＞Q＞P |
| B、R＞P＞Q |
| C、P＞R＞Q |
| D、Q＞P＞R |
如图1是牡一中高二学年每天购买烤肠数量的茎叶图，第1天到第14天的购买数量依次记为A1，A2，…，A14．图2是统计茎叶图中烤肠数量在一定范围内购买次数的一个算法流程图，那么算法流程图输出的结果是（ ）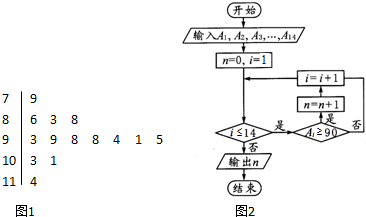
| A、7 | B、8 | C、9 | D、10 |
若圆（x-3）2+（y+5）2=r2上有且只有三个点到直线4x-3y=2的距离等于l，则半径r等于（ ）
| A、3 | B、4 | C、5 | D、6 |