题目内容
8.已知[x]表示实数x的整数部分,即[x]表示不超过实数x的最大整数,如[-2,1]=-3,[π]=3,[2]=2.函数y=[x]称为高斯函数,也叫取整函数.(1)当-2≤x<-1时,函数y=[x]的值是2.
(2)当-2≤x<2时,用分段函数表示y=[x]=$\left\{\begin{array}{l}{-2,}&{-2≤x<-1}\\{-1,}&{-1≤x<0}\\{0,}&{0≤x<1}\\{1,}&{1≤x<2}\end{array}\right.$.
(3)画出函数y=[x](x∈R)的图象.
(4)画出函数y=x-[x](x∈R)的图象.
分析 (1)根据定义得y=[x]=-2,
(2)根据定义利用分段函数进行表示,
(3)根据定义利用分段函数进行表示即可,
(4)根据定义利用分段函数进行表示即可.
解答 解:(1)当-2≤x<-1时,函数y=[x]=-2.
(2)当-2≤x<2时,
若-2≤x<-1时,y=[x]=-2,
若-1≤x<0时,y=[x]=-1,
若0≤x<1时,y=[x]=0,
若1≤x<2时,y=[x]=1,
用分段函数表示y=[x]=$\left\{\begin{array}{l}{-2,}&{-2≤x<-1}\\{-1,}&{-1≤x<0}\\{0,}&{0≤x<1}\\{1,}&{1≤x<2}\end{array}\right.$.
(3)由题意得当n≤x<n+1时,y=[x]=n,
则对应的图象为:
(4)当n≤x<n+1时,y=x-[x]=x-n,
则y=x-[x]=$\left\{\begin{array}{l}{…}&{…}\\{x-2,}&{-2≤x≤-1}\\{x-1,}&{-1≤x<0}\\{x,}&{0≤x<1}\\{x+1,}&{1≤x<2}\\{…}&{…}\\{\;}&{\;}\end{array}\right.$,则对应的图象为: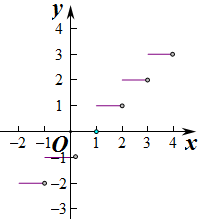
故答案为:(1)2,(2)$\left\{\begin{array}{l}{-2,}&{-2≤x<-1}\\{-1,}&{-1≤x<0}\\{0,}&{0≤x<1}\\{1,}&{1≤x<2}\end{array}\right.$.
点评 本题主要考查函数的图象的应用,结合函数的新定义表示成分段函数形式是解决本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
18.为了调查每天微信用户使用微信的时间,某经销化妆品分微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| 微信控 | 非微信控 | 合计 | |
| 男性 | 26 | 24 | 50 |
| 女性 | 30 | 20 | 50 |
| 合计 | 56 | 44 | 100 |
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜各1份,再从抽取的这5人中再随机抽取3人赠送200元的护肤品套装,记这3人中“微信控”的人数为X,试求X的分布列和数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
参考数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
3.若数列{an}满足3an+1=3an+1,则数列是( )
| A. | 公差为1的等差数列 | B. | 公差为$\frac{1}{3}$的等差数列 | ||
| C. | 公差为-$\frac{1}{3}$的等差数列 | D. | 不是等差数列 |
