题目内容
△ABC中,若cosC=2sinAsinB-1则△ABC的形状一定是( )
| A、直角三角形 |
| B、等边三角形 |
| C、等腰直角三角形 |
| D、等腰三角形 |
考点:三角形的形状判断
专题:解三角形
分析:由内角和定理得C=π-(A+B),利用两角和差的余弦公式、诱导公式化简式子,根据特殊角的余弦值判断出角之间的关系,即可得三角形的形状.
解答:
解:由A+B+C=π得,C=π-(A+B),则cosC=-cos(A+B),
所以cosC=2sinAsinB-1化为:-cos(A+B)=2sinAsinB-1,
即-cosAcosB+sinAsinB=2sinAsinB-1,
化简得,cos(A-B)=1,
所以A=B,
则△ABC是等腰三角形,
故选:D.
所以cosC=2sinAsinB-1化为:-cos(A+B)=2sinAsinB-1,
即-cosAcosB+sinAsinB=2sinAsinB-1,
化简得,cos(A-B)=1,
所以A=B,
则△ABC是等腰三角形,
故选:D.
点评:本题考查两角和差的余弦公式、诱导公式的应用,求得cos(A-B)=1,是解题的关键,属于中档题.

练习册系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,f(x)递减,都有f(x)≥0,则a=f(2010),b=f(
),c=-f(
)的大小关系是( )
| 5 |
| 4 |
| 1 |
| 2 |
| A、b<c<a |
| B、c<b<a |
| C、a<c<b |
| D、a<b<c |
已知圆柱的底面半径为2,高为3,用一个平面去截,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )
A、[
| ||
B、(0,
| ||
C、[
| ||
D、(0,
|
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2013(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
函数f(x)=x2+2x-1,x∈[-2,2]的值域为( )
A、(
| ||||
| B、(1,2) | ||||
| C、[-2,7] | ||||
| D、[-1,7] |
在极坐标系中,圆C的圆心为(6,
),半径为5,直线θ=α(0≤α≤
,ρ∈R)被圆截得的弦长为8,则α的值为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
“双曲线的方程为
-
=1”是“双曲线的渐近线方程为y=±
x”的( )
| x2 |
| 9 |
| y2 |
| 16 |
| 4 |
| 3 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知△ABC中,AB=AC=5,BC=6,则△ABC的面积为( )
| A、12 | B、15 | C、20 | D、25 |
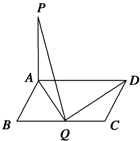 如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )
如图所示,已知矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥QD,则a=( )