题目内容
计算cos45°cos15°-sin45°cos75°的结果是 ．
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：由诱导公式和两角和的余弦公式可得原式=cos（45°+15°）=cos60°=
| 1 |
| 2 |
解答：
解：由诱导公式可得cos75°=cos（90°-15°）=sin15°，
∴cos45°cos15°-sin45°cos75°
=cos45°cos15°-sin45°sin15°
=cos（45°+15°）=cos60°=
故答案为：
∴cos45°cos15°-sin45°cos75°
=cos45°cos15°-sin45°sin15°
=cos（45°+15°）=cos60°=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查两角和与差的余弦公式，涉及诱导公式，属基础题．
练习册系列答案
相关题目
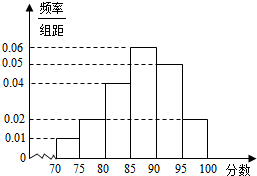某校为规范学生的行为，制定出一套科学有效的“德语百分制量化考核制度”，一领导小组将该校高三年级1200个学生随机编号为1、2、…、1200，现将编号能被30整除的40名学生抽取出来进行座谈，并将他们的考核分分成六段：[70，75），[75，80），[80，85），[85，90），[90，95），[95，100]，统计后得到如图的频率分布直方图：