Question

三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，AC=BC=1，PA=

3

，则该三棱锥外接球的表面积为（　　）

• A、5π
• B、

  2

  π
• C、20π
• D、4π

Answer 1

考点：球的体积和表面积

专题：空间位置关系与距离,球

分析：根据题意，证出BC⊥平面SAB，可得BC⊥PB，得Rt△BPC的中线OB=

1

2

PC，同理得到OA=

1

2

PC，因此O是三棱锥S-ABC的外接球心．利用勾股定理结合题中数据算出PC=

5

，得外接球半径R=

5

2

，从而得到所求外接球的表面积

解答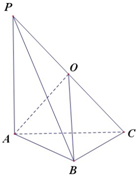： 解：取PC的中点O，连结OA、OB
∵PA⊥平面ABC，AC?平面ABC，
∴PA⊥AC，可得Rt△APC中，中线OA=

1

2

PC
又∵PA⊥BC，AB⊥BC，PA、AB是平PSAB内的相交直线
∴BC⊥平面PAB，可得BC⊥PB
因此Rt△BSC中，中线OB=

1

2

PC
∴O是三棱锥P-ABC的外接球心，
∵Rt△PCA中，AC=

2

，PA=

3

∴PC=

5

，可得外接球半径R=

1

2

PC=

5

2

∴外接球的表面积S=4πR²=5π
故选A．

点评：本题在特殊三棱锥中求外接球的表面积，着重考查了线面垂直的判定与性质、勾股定理和球的表面积公式等知识，属于中档题．