题目内容
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”.给出下列函数:
①f(x)=sinx-cosx;
②f(x)=
(sinx+cosx);
③f(x)=
sinx+2;
④f(x)=sinx.
其中“互为生成函数”的是 .
①f(x)=sinx-cosx;
②f(x)=
| 2 |
③f(x)=
| 2 |
④f(x)=sinx.
其中“互为生成函数”的是
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用函数y=Asin(ωx+∅)+b 的图象在平移过程中A和ω一定不变,可得①③互为生成的函数.
解答:
解:根据题意,两个y=Asin(ωx+∅)+b 型函数互为生成的函数的条件是,这两个函数的解析式中的A和ω相同,
∵①f(x)=sinx-cosx=
sin(x-
),②f(x)=
(sinx+cosx)=2sin(x+
),
③f(x)=
sinx+2,④f(x)=sinx.
故①③两个函数解析式中的A和ω相同,故这两个函数的图象通过平移能够完全重合.
故①③互为生成的函数,
故答案为:①③.
∵①f(x)=sinx-cosx=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
③f(x)=
| 2 |
故①③两个函数解析式中的A和ω相同,故这两个函数的图象通过平移能够完全重合.
故①③互为生成的函数,
故答案为:①③.
点评:本题考查函数y=Asin(ωx+∅)+b 的图象变换,应用了此函数图象在平移过程中A和ω不变,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
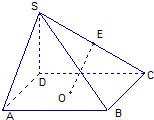 已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.
已知四棱锥S-ABCD中,底面ABCD为正方形,SD⊥DA,E为SC的中点,O为正方形ABCD的中心,AB=SD=6.