题目内容
已知数列{an},{bn}都为等比数列,公比分别为q1,q2,则数列{an+bn},{anbn},{
}是否为等比数列?公比为多少?
| an |
| bn |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由题意,an=a1q1n-1,bn=b1q2n-1,则利用等比数列的定义,即可得出结论.
解答:
解:由题意,an=a1q1n-1,bn=b1q2n-1,则
an+bn=a1q1n-1+b1q2n-1,q1=q2时,为等比数列,公比为q1;
anbn=a1q1n-1•b1q2n-1=a1b1(q1q2)n-1,为等比数列,公比为q1q2;
=a1q1n-1÷b1q2n-1=
(
)n-1,为等比数列,公比为
.
an+bn=a1q1n-1+b1q2n-1,q1=q2时,为等比数列,公比为q1;
anbn=a1q1n-1•b1q2n-1=a1b1(q1q2)n-1,为等比数列,公比为q1q2;
| an |
| bn |
| a1 |
| b1 |
| q1 |
| q2 |
| q1 |
| q2 |
点评:本题考查等比数列的定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、有两个面互相平行,其余各面都是平行四边形的几何体是棱柱 |
| B、用一个平面去截一个圆锥,只能得到一个圆锥和一个圆台 |
| C、有一个面是多边形,其余面都是三角形的几何体是棱锥 |
| D、将一个直角三角形绕其一条直角边旋转一周,所得圆锥母线长等于斜边长 |
一个几何体的三视图如图所示,则该几何体的正视图面积为( )


| A、2+3π | ||
B、2+
| ||
C、4+
| ||
| D、4+π |

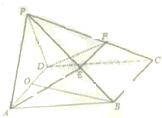 如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.
如图,已知平面PAD⊥平面ABCD,ABCD为菱形,∠BAD=60°,O是线段AD的中点,E是PB上一点,过直线AD与点E的平面与平面PBC的交线是EF.