题目内容
“a=0是f(x)=
为奇函数“的( )
| x+a |
| |x|-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:函数的性质及应用,简易逻辑
分析:先求f(x)的定义域,然后a=0时求出f(x),并容易判断此时f(x)的奇偶性;而由f(x)是奇函数,便有f(-x)=-f(x),所以能够求出a=0,这样便可得到“a=0”是“f(x)=
为奇函数”的什么条件.
| x+a |
| |x|-1 |
解答:
解:(1)f(x)的定义域为{x|x≠±1},若a=0,f(x)=
;
∴f(-x)=
=-f(x);
∴f(x)是奇函数;
a=0是f(x)=
为奇函数的充分条件;
(2)若f(x)=
是奇函数,则:
f(-x)=
=
;
∴a=-a;
∴a=0;
∴“a=0”是“f(x)=
为奇函数”的必要条件;
综合(1)(2)得“a=0“是“f(x)=
为奇函数“的充要条件.
故选C.
| x |
| |x|-1 |
∴f(-x)=
| -x |
| |x|-1 |
∴f(x)是奇函数;
a=0是f(x)=
| x+a |
| |x|-1 |
(2)若f(x)=
| x+a |
| |x|-1 |
f(-x)=
| -x+a |
| |x|-1 |
| -x-a |
| |x|-1 |
∴a=-a;
∴a=0;
∴“a=0”是“f(x)=
| x+a |
| |x|-1 |
综合(1)(2)得“a=0“是“f(x)=
| x+a |
| |x|-1 |
故选C.
点评:考查奇函数的定义,判断一个函数是否为奇函数的方法,以及充分条件、必要条件、充要条件的概念.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知点A在球O的表面上,过点A的作平面α,使OA与平面α成30°角,若平面α截球所得的圆面积为3π,则球O的体积为( )
A、
| ||
| B、4π | ||
C、
| ||
| D、16π |
某几何体的三视图如图所示,则该几何体的体积为( )
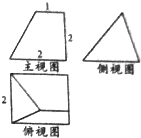

| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
下列命题是真命题的是( )
A、?x∈R使得sinxcosx=
| ||
| B、?x∈(-∞,0)使得2x>1 | ||
| C、?x∈R恒有sinx>cosx | ||
| D、?x∈(0,π)恒有x2>x-1 |
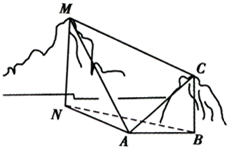 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.