题目内容
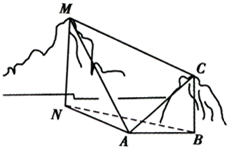如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°．已知山高BC=100m，求山高MN．考点：解三角形的实际应用
专题：解三角形
分析：由题意，可先求出AC的值，从而由正弦定理可求AM的值，在RT△MNA中，AM=100
m，∠MAN=60°，从而可求得MN的值．
| 3 |
解答：
解：在RT△ABC中，∠CAB=45°，BC=100m，所以AC=100
m．
在△AMC中，∠MAC=75°，∠MCA=60°，从而∠AMC=45°，
由正弦定理得，
=
，因此AM=100
m．
在RT△MNA中，AM=100
m，∠MAN=60°，由
=sin60°
得MN=100
×
=150m．
| 2 |
在△AMC中，∠MAC=75°，∠MCA=60°，从而∠AMC=45°，
由正弦定理得，
| AC |
| sin45° |
| AM |
| sin60° |
| 3 |
在RT△MNA中，AM=100
| 3 |
| MN |
| AM |
得MN=100
| 3 |
| ||
| 2 |
点评：本题主要考察了正弦定理的应用，考察了解三角形的实际应用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中为真命题的个数（ ）
①若m⊥α，m∥n，n∥β，则α⊥β；
②若α⊥β，m?α，m⊥β，则m∥α；
③若m⊥β，m?α，则 α⊥β；
④若α⊥β，m?α，n?β，则m⊥n．
①若m⊥α，m∥n，n∥β，则α⊥β；
②若α⊥β，m?α，m⊥β，则m∥α；
③若m⊥β，m?α，则 α⊥β；
④若α⊥β，m?α，n?β，则m⊥n．
| A、0个 | B、1个 | C、2个 | D、3个 |
“a=0是f（x）=
为奇函数“的（ ）
| x+a |
| |x|-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
不等式x2-3x＜0的解集是（ ）
| A、（-∞，0） |
| B、（0，3） |
| C、（-∞，0）∪（3，+∞） |
| D、（3，+∞） |
直线y=2x-1在y轴上的截距是（ ）
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|