题目内容
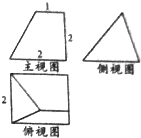
某几何体的三视图如图所示,则该几何体的体积为( )

| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,该几何体为直三棱柱切去一个三棱锥得到.
解答:
解:由题意,该几何体为直三棱柱切去一个三棱锥得到.
原直三棱柱的体积为V1=
×2×2×2=4,
三棱锥的体积为V2=
×
×2×2×1=
,
则该几何体的体积为4-
=
,
故选D.
原直三棱柱的体积为V1=
| 1 |
| 2 |
三棱锥的体积为V2=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
则该几何体的体积为4-
| 2 |
| 3 |
| 10 |
| 3 |
故选D.
点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=(
)x-log2x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)( )
| 1 |
| 3 |
| A、恒为负值 | B、等于0 |
| C、恒为正值 | D、不大于0 |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中为真命题的个数( )
①若m⊥α,m∥n,n∥β,则α⊥β;
②若α⊥β,m?α,m⊥β,则m∥α;
③若m⊥β,m?α,则 α⊥β;
④若α⊥β,m?α,n?β,则m⊥n.
①若m⊥α,m∥n,n∥β,则α⊥β;
②若α⊥β,m?α,m⊥β,则m∥α;
③若m⊥β,m?α,则 α⊥β;
④若α⊥β,m?α,n?β,则m⊥n.
| A、0个 | B、1个 | C、2个 | D、3个 |
“a=0是f(x)=
为奇函数“的( )
| x+a |
| |x|-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
