题目内容
计算下列定积分:
(1)
dx
(2)
dx
(3)
dx.
(1)
| ∫ | 1 -1 |
| x | ||
|
(2)
| ∫ | 1 0 |
| ex |
| e2x+1 |
(3)
| ∫ | e 1 |
| 2+lnx |
| x |
考点:定积分
专题:导数的概念及应用
分析:将被积函数变形,利用换元的思想转化为我们熟悉的基本初等函数形式解答.
解答:
解;(1)设
=t,则x=
,并且t∈[1,3],
所以
dx=
(
-
)d(
)=
(t2-5)dt=
(
t3-5t)|
=-
;
(2)设ex=t,则x=lnt,
dx=
dt=arctant|
=arctane-
;
(3)
dx=
(2+lnx)d(2+lnx)=
×(2+lnx)2|
=
.
| 5-4x |
| 5-t2 |
| 4 |
所以
| ∫ | 1 -1 |
| x | ||
|
| ∫ | 3 1 |
| 5 |
| 4t |
| t |
| 4 |
| 5-t2 |
| 4 |
| 1 |
| 8 |
| ∫ | 3 1 |
| 1 |
| 8 |
| 1 |
| 3 |
3 1 |
| 1 |
| 6 |
(2)设ex=t,则x=lnt,
| ∫ | 1 0 |
| ex |
| e2x+1 |
| ∫ | e 1 |
| 1 |
| 1+t2 |
e 1 |
| π |
| 4 |
(3)
| ∫ | e 1 |
| 2+lnx |
| x |
| ∫ | e 1 |
| 1 |
| 2 |
e 1 |
| 5 |
| 2 |
点评:本题考查了定积分的计算,关键是将所求转化为熟知的基本初等函数的导数,进一步求定积分.

练习册系列答案
相关题目
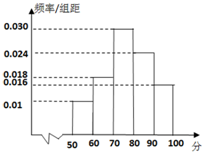 某校为了解高一年段期中考试数学科的情况,从高一的所有数学试卷中随机抽取n份试卷进行分析,得到数学成绩频率分布直方图如下图,其中成绩在[70,80)的人数为15,规定:成绩≥80分为优秀.
某校为了解高一年段期中考试数学科的情况,从高一的所有数学试卷中随机抽取n份试卷进行分析,得到数学成绩频率分布直方图如下图,其中成绩在[70,80)的人数为15,规定:成绩≥80分为优秀.