题目内容
15.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点分别为F1、F2.左、右顶点分别为A、B,虚轴的上、下端点分别为C、D.若线段BC与双曲线的渐近线的交点为E,且∠BF1E=∠CF1E,则双曲线的离心率为( )| A. | 1+$\sqrt{6}$ | B. | 1+$\sqrt{5}$ | C. | 1+$\sqrt{3}$ | D. | 1+$\sqrt{2}$ |
分析 求出双曲线的渐近线方程,求得CB的方程,解得E的坐标,即为中点,运用等腰三角形的性质,可得CF1=BF1,再由两点的距离公式和离心率公式,解方程可得所求值.
解答 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
由B(a,0),C(0,b),可得直线CB的方程为bx+ay=ab,
联立渐近线方程y=$\frac{b}{a}$x,解得E($\frac{a}{2}$,$\frac{b}{2}$),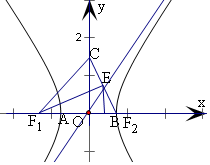
即有E为CB的中点,
由∠BF1E=∠CF1E,
即F1E平分∠CF1B,
可得三角形CF1B为等腰三角形,
即有CF1=BF1,即$\sqrt{{b}^{2}+{c}^{2}}$=a+c,
又a2+b2=c2,可得c2=2a2+2ac,
由e=$\frac{c}{a}$,可得e2-2e-2=0,
解得e=1+$\sqrt{3}$.
故选:C.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的渐近线方程,等腰三角形的性质,以及方程的思想,考查运算能力,属于中档题.

练习册系列答案
相关题目
20.在数列{an}中,对任意n∈N*,都有an+1-2an=0,则$\frac{{2{a_1}+{a_2}}}{{2{a_3}+{a_4}}}$等于( )
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
4.在等比数列{an}中,a3a7=4a4=4,则a8等于( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
5.已知数列{an}中,a1=2,当n≥2时,$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+n-1,设bn=$\frac{{a}_{n}}{{2}^{n}}$-1,则$\frac{1}{{b}_{2}}$+$\frac{1}{{b}_{3}}$+…+$\frac{1}{{b}_{20}}$等于( )
| A. | $\frac{19}{10}$ | B. | $\frac{29}{20}$ | C. | $\frac{40}{21}$ | D. | $\frac{36}{19}$ |