题目内容
4.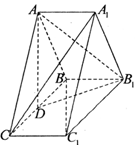 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,D为棱BC的中点,AB=AC,BC=$\sqrt{2}A{A_1}$,求证:(1)A1C∥平面ADB1;
(2)BC1⊥平面ADB1.
分析 (1)如图,连接A1B交AB1于M,可得DM∥A1C,即可证得A1C∥平面ADB1,
(2)三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,可得AD⊥BB1,即可得AD⊥BC1,在矩形BCC1B1中,由△BDB1∽△B1BC1,可得$∠{C}_{1}B{B}_{1}+∠B{B}_{1}D=9{0}^{0}$.即可得BC1⊥DB1,BC1⊥平面ADB1.
解答 解:(1)证明:如图,连接A1B交AB1于M,
则M为A1B中点,连接DM,
∵D为棱BC的中点,∴DM∥A1C,
又A1C?平面ADB1,DM?平面ADB1
∴A1C∥平面ADB1,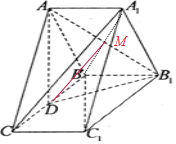
(2)三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,可得AD⊥BB1
∵D为棱BC的中点,AB=AC,∴AD⊥面BCC1B1,即AD⊥BC1,
在矩形BCC1B1中,∵BC=$\sqrt{2}A{A_1}$,∴$\frac{B{B}_{1}}{DB}=\sqrt{2},\frac{{B}_{1}{C}_{1}}{B{B}_{1}}=\sqrt{2}$
∴△DBB1∽△BB1C1⇒∠BDB1=∠B1BC1,∠BB1D=∠BC1B1,即$∠{C}_{1}B{B}_{1}+∠B{B}_{1}D=9{0}^{0}$.
∴BC1⊥DB1,且AD∩DB1=D,∴BC1⊥平面ADB1.
点评 本题考查了空间线面平行的判定,线面垂直的判定,属于中档题.

练习册系列答案
相关题目
15.红星超市为了了解顾客一次购买某牛奶制品的数量(单位:盒)及结算的时间(单位:分钟)等信息,随机收集了在该超市购买牛奶制品的50位顾客的相关数据,如表所示:
(Ⅰ)请估计这50位顾客购买牛奶制品的结算时间的平均值;并求一位顾客的结算时间小于结算时间平均值的概率;
(Ⅱ)从购买牛奶制品的数量不少于10盒的顾客中任选两人,求两位顾客的结算时间之和超过3.5分钟的概率.
| 一次购物数量 | 1至2盒 | 3至5盒 | 6至9盒 | 10至17盒 | 18至25盒 |
| 顾客数量(人) | 20 | 14 | 10 | 2 | 4 |
| 结算的时间(分钟/人) | 1 | 1.5 | 2 | 1.5 | 2 |
(Ⅱ)从购买牛奶制品的数量不少于10盒的顾客中任选两人,求两位顾客的结算时间之和超过3.5分钟的概率.
19.已知f(x)是定义在R上的奇函数,且f(x+2)=f(x-2);当0≤x≤1时,f(x)=$\sqrt{x}$,则f(1)+f(2)+f(3)+…+f(2017)等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
8.4个不同的小球全部随意放入3个不同的盒子里,使每个盒子都不空的放法种数为( )
| A. | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B. | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C. | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D. | ${C}_{4}^{2}{A}_{3}^{3}$ |