题目内容
3.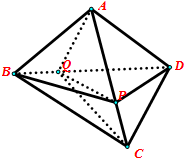 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )| A. | 22 | B. | 34 | C. | 32 | D. | 40 |
分析 由$\frac{BQ}{DQ}$=$\frac{{S}_{△BCQ}}{{S}_{△CDQ}}$=$\frac{BQ}{DQ}=\frac{1}{4}$,$\frac{{V}_{P-ABQ}}{{V}_{P-ADQ}}=\frac{{S}_{△ABQ}}{{S}_{△ADQ}}=\frac{BQ}{DQ}$得出VA-DPQ,则VA-BCD为四个小棱锥的体积和.
解答 解:设P到平面BCD的距离为h,
则VB-CPQ=VP-BCQ=$\frac{1}{3}{S}_{△BCQ}•h$,VQ-PCD=VP-CDQ=$\frac{1}{3}{S}_{△CDQ}•h$,
∴$\frac{{S}_{△BCQ}}{{S}_{△CDQ}}$=$\frac{{V}_{B-CPQ}}{{V}_{Q-PCD}}$=$\frac{2}{8}=\frac{1}{4}$,
∴$\frac{BQ}{DQ}$=$\frac{{S}_{△BCQ}}{{S}_{△CDQ}}$=$\frac{1}{4}$,
∴$\frac{{V}_{P-ABQ}}{{V}_{P-ADQ}}=\frac{{S}_{△ABQ}}{{S}_{△ADQ}}=\frac{BQ}{DQ}$=$\frac{1}{4}$,
∴VA-DPQ=4VP-ABQ=24,
∴VA-BCD=6+2+8+24=40.
故选:D.
点评 本题考查了棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
18.已知点P是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1上一点,若PF1⊥PF2,则△PF1F2的面积为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
8.下列命题中的假命题是( )
| A. | ?x∈R,lgx=0 | B. | ?x∈R,x3>0 | C. | ?x∈R,tanx=1 | D. | ?x∈R,2x>0 |
14.函数f(x)=ax2+bx(a>0,b>0)在点(1,f(1))处的切线斜率为2,则$\frac{2a+b}{ab}$的最小值是( )
| A. | 2 | B. | 3$\sqrt{2}$ | C. | 1 | D. | 4 |
 如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题:
如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC上,FG∥BC,AB=AE=2,∠EAB=60°,有以下四个命题: