题目内容
8.下列命题中的假命题是( )| A. | ?x∈R,lgx=0 | B. | ?x∈R,x3>0 | C. | ?x∈R,tanx=1 | D. | ?x∈R,2x>0 |
分析 利用特例判断A的正误,反例判断B的正误;特例判断C的正误;指数函数的性质判断D的正误;
解答 解:当x=1时,lgx=0,所以A正确;
当x<0时,x3<0,所以B不正确;
当x=$\frac{π}{4}$时,tanx=1,所以C正确;
由指数函数的性质可知?x∈R,2x>0恒成立,所以D正确;
故选:B.
点评 本题考查命题的真假的判断与应用,注意基本知识的熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.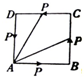 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
16.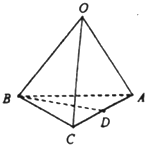 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )| A. | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
13.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的渐近线方程为( )
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
18.若复数z满足z(1-i)=2,则z=( )
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
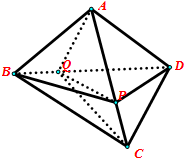 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )