题目内容
11．已知xi∈{-1，0，1}，i=1，2，3，4，5，6，则满足x1+x2+x3+x4+x5+x6=2的数组（x1，x2，x3，x4，x6）的个数为（ ）| A． | 60 | B． | 75 | C． | 90 | D． | 120 |
分析 由x1+x2+x3+x4+x5+x6=2，结合xi的取值，讨论xi所有取值的可能性，求出满足x1+x2+x3+x4+x5+x6=2的数组（x1，x2，x3，x4，x6）的个数．
解答 解：根据题意，∵x1+x2+x3+x4+x5+x6=2，xi∈{0，1，-1}，i=1，2，3，4，5，6；
∴xi中有2个1和4个0，或3个1、1个-1和2个0，或4个1和2个-1
共有${C}_{6}^{2}+{C}_{6}^{3}{C}_{3}^{2}+{C}_{6}^{4}$=90个，
∴满足x1+x2+x3+x4+x5+x6=2的数组（x1，x2，x3，x4，x6）的个数为90个．
故选：C．
点评 本题通过集合的概念，考查了排列组合的应用问题，解题时应深刻理解题意，抓住问题的关键，进行解答问题，是基础题．
练习册系列答案
相关题目
2．已知点P为圆C：x2+y2=4上的动点，A（4，0），则线段AP中点M的轨迹方程为（ ）
| A． | （x-2）2+y2=1 | B． | （x+2）2+y2=1 | C． | （x-2）2+y2=4 | D． | x2+（y-2）2=4 |
6．二项式（a-1）8的展开式中，最大的二项式系数为（ ）
| A． | C${\;}_{8}^{4}$ | B． | -C${\;}_{8}^{4}$ | C． | C${\;}_{9}^{5}$ | D． | -C${\;}_{9}^{5}$ |
16．
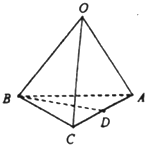如图，在三棱锥O-ABC中，点D是棱AC的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{BD}$等于（ ）
如图，在三棱锥O-ABC中，点D是棱AC的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{BD}$等于（ ）| A． | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B． | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C． | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D． | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
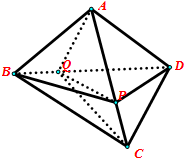如图：在三棱锥A-BCD中，P∈AC，Q∈BD，若VA-BPQ=6，VB-CPQ=2，VQ-PCD=8，则三棱锥A-BCD的体积VA-BCD为（ ）