题目内容
14.某次联欢会的抽奖规则如下:观众从一个装有8个红球和2个白球的箱子中一次摸出两个球,若都是白球,则为一等奖,若恰有一个白球,则为二等奖.那么,这名观众中奖的概率是$\frac{17}{45}$.分析 根据互斥事件、古典概型概率计算即可.
解答 解:中一等奖的概率为$\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{1}{45}$,中二等奖的概率为$\frac{{C}_{2}^{1}•{C}_{8}^{1}}{{C}_{10}^{2}}$=$\frac{16}{45}$,
∴这名观众中奖的概率是$\frac{1}{45}$+$\frac{16}{45}$=$\frac{17}{45}$
故答案为:$\frac{17}{45}$
点评 本题考查互斥事件、古典概型概率的计算,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
2.已知点P为圆C:x2+y2=4上的动点,A(4,0),则线段AP中点M的轨迹方程为( )
| A. | (x-2)2+y2=1 | B. | (x+2)2+y2=1 | C. | (x-2)2+y2=4 | D. | x2+(y-2)2=4 |
6.二项式(a-1)8的展开式中,最大的二项式系数为( )
| A. | C${\;}_{8}^{4}$ | B. | -C${\;}_{8}^{4}$ | C. | C${\;}_{9}^{5}$ | D. | -C${\;}_{9}^{5}$ |
5.函数f(x)在点x0处取得极值,则必有( )
| A. | f′(x0)=0 | B. | f′(x0)<0 | ||
| C. | f′(x0)=0且f″(x0)<0 | D. | f′(x0)或f′(x0)不存在 |
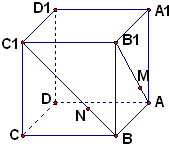 在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:
在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论: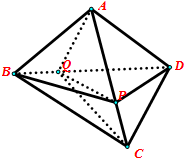 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )