题目内容
13.$\frac{2tan150°}{1-tan^{2}150°}$的值为-$\sqrt{3}$.分析 直接利用二倍角公式以及特殊角的三角函数化简求解即可.
解答 解:$\frac{2tan150°}{1-tan^{2}150°}$
=tan300°
=-tan60°=-$\sqrt{3}$.
故答案为:-$\sqrt{3}$.
点评 本题考查二倍角公式的应用,特殊角的三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
3.已知$\frac{1+2i}{a+bi}$=1-i(i为虚数单位,a,b∈R),则|a+bi|=( )
| A. | $\frac{1}{2}+\frac{3}{2}i$ | B. | 1 | C. | 2 | D. | $\frac{{\sqrt{10}}}{2}$ |
18.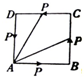 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
 如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )
如图,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过B、C、D再回到A.用x表示P点经过的路程,y表示AP的长,则当1<x<2时,$\frac{y^2}{x}$的最小值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$-2 | D. | 3$\sqrt{2}$-2 |
2.已知点P为圆C:x2+y2=4上的动点,A(4,0),则线段AP中点M的轨迹方程为( )
| A. | (x-2)2+y2=1 | B. | (x+2)2+y2=1 | C. | (x-2)2+y2=4 | D. | x2+(y-2)2=4 |
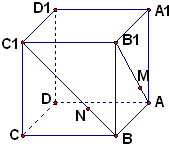 在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:
在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论: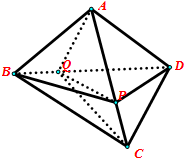 如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )
如图:在三棱锥A-BCD中,P∈AC,Q∈BD,若VA-BPQ=6,VB-CPQ=2,VQ-PCD=8,则三棱锥A-BCD的体积VA-BCD为( )