题目内容
命题“?x≠1，x2-x≠0”的否定是： ．
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，
所以命题“?x≠1，x2-x≠0”的否定是：?x≠1，x2-x=0．
故答案为：?x≠1，x2-x=0
所以命题“?x≠1，x2-x≠0”的否定是：?x≠1，x2-x=0．
故答案为：?x≠1，x2-x=0
点评：本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
函数y=
+
的定义域是（ ）
| 1-x2 |
| x2-1 |
| A、{x|-1＜x＜1} |
| B、{x|x＜-1，或x＞1} |
| C、{x|0＜x＜1} |
| D、{-1，1} |
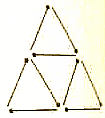用9根火柴棒搭成的图案如图所示，移动2根火柴棒，使这9根火柴棒搭成一个中心对称图形，并画出这个图形．
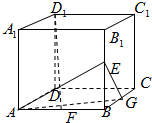如图正方体ABCD-A1B1C1D1中，E、F、G分别是BB1、AB、BC的中点．