题目内容
已知点A(2,3),B(-3,-2),若直线l过点P(1,1)与线段AB相交,则直线l的斜率k的取值范围是 .
考点:直线的斜率
专题:直线与圆
分析:画出图形,由题意得所求直线l的斜率k满足 k≥kPB 或 k≤kPA,用直线的斜率公式求出kPB 和kPA 的值,求出直线l的斜率k的取值范围.
解答:
 解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
即 k≥
=
,或 k≤
=2,∴k≤
,或k≥2,
即直线的斜率的取值范围是k≤
,或k≥2.
故答案为:k≤
,或k≥2.
 解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,即 k≥
| 1+2 |
| 1+3 |
| 3 |
| 4 |
| 1-3 |
| 1-2 |
| 3 |
| 4 |
即直线的斜率的取值范围是k≤
| 3 |
| 4 |
故答案为:k≤
| 3 |
| 4 |
点评:本题考查直线的斜率公式的应用,体现了数形结合的数学思想,解题的关键是利用了数形结合的思想,解题过程较为直观,本题类似的题目比较多.可以移动一个点的坐标,变式出其他的题目.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
函数y=(
)x+1的图象必经过点( )
| 1 |
| 2 |
| A、(0,2) |
| B、(0,1) |
| C、(-1,0) |
| D、(1,0) |
计算:
(x3+1)dx=( )
| ∫ | 2 -2 |
| A、2 | B、4 | C、8 | D、12 |
为了得到函数y=sin(2x-
)的图象,可以将函数y=cos2x的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
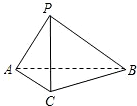 在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.