题目内容
设函数f(x)在(0,+∞)内可导,且f(ex)=x+e2x,f′(x)的最小值为 .
考点:简单复合函数的导数
专题:导数的概念及应用
分析:首先求出f(x)的解析式,再求导,最后利用基本不等式求出最小值.
解答:
解:∵f(ex)=x+e2x,
∴f(ex)=lnex+(ex)2,
∴f(x)=lnx+x2,x∈(0,+∞)
∴f′(x)=
+2x≥2
=2
,当且仅当x=
时取等号.
故答案为:2
∴f(ex)=lnex+(ex)2,
∴f(x)=lnx+x2,x∈(0,+∞)
∴f′(x)=
| 1 |
| x |
|
| 2 |
| ||
| 2 |
故答案为:2
| 2 |
点评:本题主要考查了函数解析式的求法,求导的运算法则,以及基本不等式,知识点比较多,属于中档题.

练习册系列答案
相关题目
已知正实数x,y满足z=(x-y)2+3y2,则
的最大值为( )
| xy |
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知集合M={x|x2-2x-3≤0},N={x|y=
},则M∩N=( )
| x-2 |
| A、{x|-1≤x≤3} |
| B、{x|2≤x≤3} |
| C、{x|-1≤x≤2} |
| D、∅ |
“a>2”是“函数f(x)=loga(2-ax)在定义域内为减函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如果复数
(其中b∈R)的实部与虚部互为相反数,则b=( )
| 2-bi |
| i3 |
| A、2 | B、-2 | C、-1 | D、1 |
 如图根据频率分布直方图估计该组数据的中位数是
如图根据频率分布直方图估计该组数据的中位数是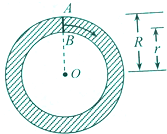 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×