题目内容
14．不等式$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$≤2$\sqrt{6}$的解集为（ ）| A． | {x|-$\sqrt{2}$≤x≤$\sqrt{2}$} | B． | {x|-$\sqrt{3}$≤x≤$\sqrt{3}$} | C． | {x|-2≤x≤2} | D． | {x|-$\sqrt{5}$≤x≤$\sqrt{5}$} |
分析 根据式子$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$ 表示x轴上的点（x，0）对应点到A（-2，1）、B（2，1）对应点的距离之和，x轴上的点（±$\sqrt{3}$，0）到A（-2，1）、B（2，1）对应点的距离之和正好等于2$\sqrt{6}$，从而求得原不等式的解集．
解答 解：式子$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$ 表示x轴上的点（x，0）对应点到A（-2，1）、B（2，1）对应点的距离之和．
由于x轴上的点（±$\sqrt{3}$，0）到A（-2，1）、B（2，1）对应点的距离之和正好等于2$\sqrt{6}$，
不等式$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$≤2$\sqrt{6}$的解集为{x|-$\sqrt{3}$≤x≤$\sqrt{3}$}，
故选：B．
点评 本题主要考查两点间的距离公式的应用，属于中档题．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
4．分别在区间[0，$\frac{π}{2}$]和[0，1]内任取两个实数x，y，则不等式y≤cosx恒成立的概率为（ ）
| A． | $\frac{1}{π}$ | B． | $\frac{2}{π}$ | C． | $\frac{3}{π}$ | D． | $\frac{1}{2}$ |
19．
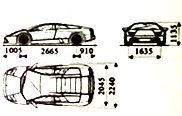髙先生新购买了辆小汽车，汽车的一些参数如图所示（单位：毫米），他计划把车放在车库地面的中间，四周边缘外前后左右各留半米且上方留空一米，则该车库的体积（保留小数点后两位数字）至少为（ ）
髙先生新购买了辆小汽车，汽车的一些参数如图所示（单位：毫米），他计划把车放在车库地面的中间，四周边缘外前后左右各留半米且上方留空一米，则该车库的体积（保留小数点后两位数字）至少为（ ）| A． | 11.64立方米 | B． | 36.28立方米 | C． | 38.60立方米 | D． | 40.70立方米 |