题目内容
19.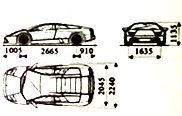 髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )
髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )| A. | 11.64立方米 | B. | 36.28立方米 | C. | 38.60立方米 | D. | 40.70立方米 |
分析 由图求得汽车的长、宽、高,再由四周边缘外前后左右各留半米且上方留空一米,可得车库的长,宽、高,再由体积公式计算即可得到所求值.
解答 解:该车的长为1005+2665+910=4580mm=4.58m,
宽为2240mm=2.24m,最高处为1135mm=1.135m,
则该车库的体积至少为5.58×3.24×2.135≈38.60m3,
故选:C.
点评 本题考查体积公式的运用,考查应用题的解法,注意认真审题,准确计算,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列函数为偶函数的是( )
| A. | f(x)=x | B. | f(x)=x3 | C. | f(x)=x2,x∈(-5,5] | D. | f(x)=4 |
10.己知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
| A. | 2 | B. | 3 | C. | $\frac{11}{5}$ | D. | $\frac{37}{16}$ |
7.根据统计知识,则不正确的命题是( )
| A. | 传染病医院感染禽流感的医务人员数与医院收治的禽流感病人数是具有相关关系的两个变量 | |
| B. | 从参加高三模拟考试的1200名学生中,随机抽取100人了解试卷难易情况可以用系统抽样 | |
| C. | 回归直线$\widehat{y}$=bx+a必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| D. | 对一组数据进行适当整理后,众数所在的一组频数最大 |
14.不等式$\sqrt{{x}^{2}+4x+5}$+$\sqrt{{x}^{2}-4x+5}$≤2$\sqrt{6}$的解集为( )
| A. | {x|-$\sqrt{2}$≤x≤$\sqrt{2}$} | B. | {x|-$\sqrt{3}$≤x≤$\sqrt{3}$} | C. | {x|-2≤x≤2} | D. | {x|-$\sqrt{5}$≤x≤$\sqrt{5}$} |
11.已知m,n,l为不同的直线,α,β,γ为不同的平面,则下列命题正确的是( )
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m∥n,n∥α,则m∥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若α⊥γ,β⊥γ,则α∥β |
8.点A(-1,$\sqrt{3}$),B(1,3$\sqrt{3}$),则直线AB的倾斜角为( )
| A. | 30° | B. | 150° | C. | 60° | D. | 120° |
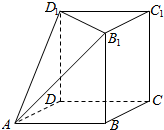 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.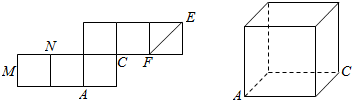 如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点
如图,是一个正方体的平面展开图及该正方形的直观图的示意图,其中M是所在棱的中点