题目内容
8.已知P是椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上任意一点,过椭圆的右顶点A和上顶点B分别作x轴和y轴的垂线,两垂线交于点C,过P作AC,BC的平行线交BC于点M,交AC于点N,交AB于点D,E,矩形PMCN的面积是S1,三角形PDE的面积是S2,则$\frac{{2{S_1}}}{S_2}$=( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{8}{5}$ |
分析 确定AB的方程,求出S△ADN、SACME.利用P(x,y)在椭圆上可知S1=S2,从而可得结论.
解答 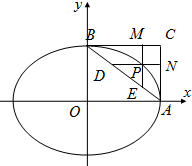 解:设P(x,y)在第一象限,则AB的方程为$\frac{x}{5}$+$\frac{y}{3}$=1,
解:设P(x,y)在第一象限,则AB的方程为$\frac{x}{5}$+$\frac{y}{3}$=1,
∴D(5-$\frac{5y}{3}$,y),E(x,3-$\frac{3x}{5}$),
∴S△ADN=$\frac{1}{2}$×$y×\frac{5y}{3}$=$\frac{5{y}^{2}}{6}$,
∴SACME=$\frac{1}{2}×$($\frac{3x}{5}+3$)×(5-x)=$\frac{3}{10}$(25-x2),
∵P(x,y)在椭圆上,∴$\frac{x^2}{25}+\frac{y^2}{9}=1$,
∴y2=9-$\frac{9{x}^{2}}{25}$,
∴$\frac{5{y}^{2}}{6}$=$\frac{3}{10}$(25-x2),
∴S△ADN=SACME,
∴S1=S2,
∴$\frac{{2{S_1}}}{S_2}$=2.
故选A.
点评 本题考查椭圆的标准方程,考查面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
18.已知不等式组$\left\{\begin{array}{l}0≤x≤π\\ y≤sinx+a\\ y≥0\end{array}\right.$所对应的平面区域面积为2+2π,则$\sqrt{3}x+2y+1$的最大值为( )
| A. | $\frac{{5\sqrt{3}π}}{6}+6$ | B. | $\sqrt{3}π+7$ | C. | 6 | D. | 7 |
20.集合A={x|x2-4=0}的子集个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
17.已知tanα,$\frac{1}{tanα}$是关于x的方程x2-kx+k2-3=0的两个实根,且3π<α<$\frac{7}{2}$π,则cosα+sinα=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
14.某校高二2班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如表数据:
(Ⅰ)求线性回归方程;
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| y | 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
(Ⅱ)该班某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
参考数据:$\overline x=17.4$,$\overline y=74.9$,$\sum_{i=1}^{10}{{x_i}^2=3182}$,$\sum_{i=1}^{10}{{y_i}^2=58375}$,$\sum_{i=1}^{10}{{x_i}{y_i}=13578}$
回归直线方程参考公式:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$.