题目内容
已知函数y=x2-2ax+a2-3．
（1）若函数在区间[3，+∞）上单调递增，求实数a的取值范围；
（2）若x∈[-1，2]，求函数最小值g（a）的函数表达式．
（1）若函数在区间[3，+∞）上单调递增，求实数a的取值范围；
（2）若x∈[-1，2]，求函数最小值g（a）的函数表达式．
考点：二次函数的性质,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：（1）根据函数在区间[3，+∞）上单调递增，得出a≤3，
（2）分类讨论求解：当a≤-1时，当a≥2时，当-1＜a＜2时．
（2）分类讨论求解：当a≤-1时，当a≥2时，当-1＜a＜2时．
解答：
解：函数y=x2-2ax+a2-3．
对称轴为x=a，
（1）∵函数在区间[3，+∞）上单调递增，
∴a≤3，
故实数a的取值范围：a≤3，
（2）∵x∈[-1，2]，
∴当a≤-1时，函数最小值g（a）=f（-1）=a2+2a-2，
当a≥2时，函数最小值g（a）=f（2）=a2-4a+1，
，函数最小值g（a）=f（a）=-3，
∴g（a）=
对称轴为x=a，
（1）∵函数在区间[3，+∞）上单调递增，
∴a≤3，
故实数a的取值范围：a≤3，
（2）∵x∈[-1，2]，
∴当a≤-1时，函数最小值g（a）=f（-1）=a2+2a-2，
当a≥2时，函数最小值g（a）=f（2）=a2-4a+1，
，函数最小值g（a）=f（a）=-3，
∴g（a）=
|
点评：本题考查了二次函数的性质，分类讨论求解最值，关键确定讨论的标准，属于容易题．
练习册系列答案
名校课堂系列答案
相关题目
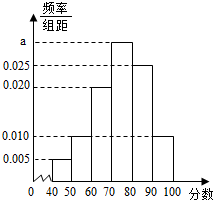为了更好的了解某校高三学生期中考试的数学成绩情况，从所有高三学生中抽取40名学生，将他们的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图．