题目内容
函数f(x)当x趋近于x0时极限存在是f(x)在点x0的某个去心领域内有界的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、即不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由极限可知前可推后,但后不能推前,由充要条件的定义可得.
解答:
解:∵函数f(x)当x趋近于x0时极限存在能够推出f(x)在点x0的某个去心领域内有界,
又∵f(x)在点x0的某个去心领域内有界不能推出当x趋近于x0时函数f(x)极限存在,
∴函数f(x)当x趋近于x0时极限存在是f(x)在点x0的某个去心领域内有界的充分不必要条件,
故选:A
又∵f(x)在点x0的某个去心领域内有界不能推出当x趋近于x0时函数f(x)极限存在,
∴函数f(x)当x趋近于x0时极限存在是f(x)在点x0的某个去心领域内有界的充分不必要条件,
故选:A
点评:本题考查充要条件,涉及极限的性质,属基础题.

练习册系列答案
相关题目
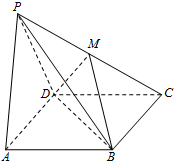 如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.