题目内容
已知函数f(x)=loga
(a>0,a≠1)
(1)求定义域.
(2)判断奇偶性并证明.
(3)当a>1时,函数f(x)在定义域上是 (填增减性,不必说明理由.)
(4)当0<a<1时,求使f(x)>0的x的取值范围.
| 1+x |
| 1-x |
(1)求定义域.
(2)判断奇偶性并证明.
(3)当a>1时,函数f(x)在定义域上是
(4)当0<a<1时,求使f(x)>0的x的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)函数f(x)=loga
(a>0,a≠1)根据对数函数的概念可得;
>0,解不等式即可的定义域.
(2)利用奇偶性概念判断,f(-x)与f(x)比较,
(3)根据对数函数单调性解不等式:loga
>0,loga
>log
,即可求出x的范围.
| 1+x |
| 1-x |
| 1+x |
| 1-x |
(2)利用奇偶性概念判断,f(-x)与f(x)比较,
(3)根据对数函数单调性解不等式:loga
| 1+x |
| 1-x |
| 1+x |
| 1-x |
1 a |
解答:
解:(1)由题意知
>0,解得:-1<x<1,
故函数f(x)的定义域为{x|-1<x<1}.
(2)由(1)知定义域关于原点对称,对于定义域内的每一个x,
由f(x)+f(-x)=loga
+loga
=loga
=loga1=0
可知:f(-x)=-f(x),
因此该函数为奇函数.
(3)当a>1时,f(x)在(-1,1)上是增函数.运用单调性定义证明判断,主要作差判断.
(4)证明:任取x1,x2∈(-1,1),且x1<x2
f(x1)-f(x2)=loga
-loga
=loga
因为
-1=
又-1<x1<x2<1,所以
<0,
因此有
<1.
又a>1,所以loga
<0,
即f(x1)<f(x2).
所以当a>1时,f(x)在(-1,1)上是增函数.
(4)f(x)>0即loga
>0,loga
,>log
,
因为0<a<1,所以由对数函数的单调性知0<
<1,解得-1<x<0.
故对于0<a<1,当x∈(-1,0)时,f(x)>0.
| 1+x |
| 1-x |
故函数f(x)的定义域为{x|-1<x<1}.
(2)由(1)知定义域关于原点对称,对于定义域内的每一个x,
由f(x)+f(-x)=loga
| 1+x |
| 1-x |
| 1-x |
| 1+x |
| (1+x)(1-x) |
| (1-x)(1+x) |
可知:f(-x)=-f(x),
因此该函数为奇函数.
(3)当a>1时,f(x)在(-1,1)上是增函数.运用单调性定义证明判断,主要作差判断.
(4)证明:任取x1,x2∈(-1,1),且x1<x2
f(x1)-f(x2)=loga
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
因为
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
| 2(x1-x2) |
| (1-x1)(1+x2) |
又-1<x1<x2<1,所以
| 2(x1-x2) |
| (1-x1)(1+x2) |
因此有
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
又a>1,所以loga
| (1+x1)(1-x2) |
| (1-x1)(1+x2) |
即f(x1)<f(x2).
所以当a>1时,f(x)在(-1,1)上是增函数.
(4)f(x)>0即loga
| 1+x |
| 1-x |
| 1+x |
| 1-x |
1 a |
因为0<a<1,所以由对数函数的单调性知0<
| 1+x |
| 1-x |
故对于0<a<1,当x∈(-1,0)时,f(x)>0.
点评:本题综合考查了对数函数的性质,融合了函数奇偶性,单调性,解不等式等问题,难度较大.

练习册系列答案
相关题目
已知函数f(x)=(x-a)(x-b),(a>b)的图象如图所示,则g(x)=ax+b的图象经过( )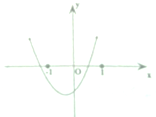

| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |
在区间[0,1]上随机取一个数x,使y=3x-1的值介于1与2之间的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2x满足( )
| A、f(xy)=f(x)+f(y) |
| B、f(xy)=f(x)•f(y) |
| C、f(x+y)=f(x)+f(y) |
| D、f(x+y)=f(x)•f(y) |