题目内容
下列函数中，既是奇函数又在（0，+∞）上单调递减的函数是（ ）
A、y=
| ||
| B、y=e-x | ||
| C、y=-tanx | ||
| D、y=|x| |
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：利用奇偶函数的定义判断奇偶性，再确定函数的单调性，即可得到结论．
解答：
解：对于A，函数是奇函数，在区间（0，+∞）上递减，故A正确；
对于B，函数不是奇函数也不是偶函数，故B不正确；
对于C，函数是奇函数，在（kπ-
，kπ+
）上递减，但在（0，+∞）上不一定单调递减，故C不正确；
对于D，函数是偶函数，故D不正确．
故选：A．
对于B，函数不是奇函数也不是偶函数，故B不正确；
对于C，函数是奇函数，在（kπ-
| π |
| 2 |
| π |
| 2 |
对于D，函数是偶函数，故D不正确．
故选：A．
点评：本题考查函数单调性与奇偶性的结合，正确运用定义是关键．
练习册系列答案
孟建平名校考卷系列答案
相关题目
集合M={x|x=
±45°，k∈z}，P={x|x=
±90°，k∈Z}，则M、P之间的关系为（ ）
| k•180° |
| 2 |
| k•180° |
| 4 |
| A、M=P | B、M⊆P? |
| C、M?P | D、M∩P=∅ |
等比数列{an}中，已知a3•a10=8a52，a2=2，则a1=（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
已知函数f（x）=（x-a）（x-b），（a＞b）的图象如图所示，则g（x）=ax+b的图象经过（ ）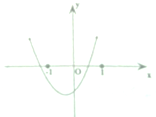
| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第一、三、四象限 |
| D、第二、三、四象限 |
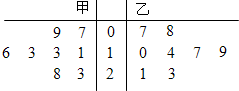某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图：若以甲、乙两名队员得分的频率作为概率，假设甲、乙两名队员在同一场比赛中的得分互不影响．