题目内容
18．现有A，B，C三种产品需要检测，产品数量如下表：| 产品 | A | B | C |
| 数量 | 800 | 800 | 1200 |
（1）求分别抽取的三种产品件数；
（2）已知被抽取的A，B，C三种产品中，一等品分别有1件、2件、2件，现再从已抽取的A，B，C三件产品中各抽取1件，求3件产品都是一等品的概率．
分析 （1）设A、B产品均抽取了x件，C产品抽取了7-2x件，利用用分层抽样的方法能求出分别抽取的三种产品件数．
（2）记抽取的A产品为a1，a2，其中a1为一等品，抽取的B产品为b1，b2，两件均为一等品，抽取的C产品为c1，c2，c3，其中c1，c2为一等品，由此能求出3件产品均为一等品的概率．
解答 解：（1）设A、B产品均抽取了x件，C产品抽取了7-2x件，
则有$\frac{x}{800}$=$\frac{7-x}{1200}$，解得x=2，
∴A、B产品分别抽取了2件，C产品抽取了3件．
（2）记抽取的A产品为a1，a2，其中a1为一等品，
抽取的B产品为b1，b2，两件均为一等品，
抽取的C产品为c1，c2，c3，其中c1，c2为一等品，
从三种产品中各取一件，基本事件数n=2×2×3=12，
其中三个都是一等品的基本事件有：{a1，b1，c1}，{a1，b1，c2}，{a1，b2，c1}，{a1，b2，c2}，共4件，
∴3件产品均为一等品的概率p=$\frac{4}{12}$=$\frac{1}{3}$．
点评 本题考查分层抽样方法的应用，考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x-y+2≥0}\end{array}\right.$确定的平面区域记为Ω1，不等式组$\left\{\begin{array}{l}{x+y-1≤0}\\{x+y+2≥0}\end{array}\right.$确定的平面区域记为Ω2，在Ω1中随机取一点，则该点恰好在Ω2内的概率为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{4}$ | D． | $\frac{7}{8}$ |
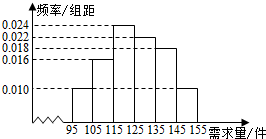某商场经销某一种电器商品，在一个销售季度内，每售出一件该商品获利200元，未售出的商品，每件亏损100元，根据以往资料，得到销售季度内市场需求量的频率分布直方图，如图所示，现在经销商为下一个销售季度购进了125件该种电器，以n（单位：件；95≤n≤155）表示下一个销售季度市场需求量，Y（单位：元）表示下一个销售季度内销售 该电器的利润．