题目内容
6.给出方程组$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=1+tsinθ}\end{array}\right.$当t为参数时动点(x,y)的轨迹方程为曲线C1,当θ为参数时动点(x,y)的轨迹曲线C2,且C1与C2的一个公共点为(1+$\sqrt{2}$,1+$\sqrt{2}$).(1)求C1与C2的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C2的极坐标方程以及C1与C2交点的极坐标(ρ≥0,0≤θ≤2π)
分析 (1)根据所给参数方程,消去相应的参数即可得到相应的普通方程;
(2)结合(1),直接写出相应曲线C2的极坐标方程,然后,将所给交点的坐标化为极坐标形式即可.
解答 解:(1)根据参数方程$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=1+tsinθ}\end{array}\right.$,消去参数t,得
$\frac{x-1}{y-1}=\frac{cosθ}{sinθ}$,
∴xsinθ-ycosθ+cosθ-sinθ=0,
∴曲线C1的普通方程为:xsinθ-ycosθ+cosθ-sinθ=0,
根据参数方程$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=1+tsinθ}\end{array}\right.$,消去参数θ,得
(x-1)2+(y-1)2=t2,
∴曲线C2的普通方程为:(x-1)2+(y-1)2=t2,
(2)结合(1)中曲线C2的普通方程,得
x2+y2-2x-2y-2-t2=0,
∴曲线C2的极坐标方程为:ρ2-2ρcosθ-2ρsinθ-2-t2=0,
又∵C1与C2的一个公共点为(1+$\sqrt{2}$,1+$\sqrt{2}$),
此时极角θ,满足tanθ=1,
∴θ=$\frac{π}{4}$,
∵极径ρ=$\sqrt{2×(1+\sqrt{2})^{2}}$=2+$\sqrt{2}$,
∴C1与C2交点的极坐标为(2+$\sqrt{2}$,$\frac{π}{4}$).
点评 本题综合考查了极坐标和直角坐标的互化、参数方程和普通方程的互化等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.一个年级有20个班,每个班同学从1~50排学号,为了交流学习经验,要求每班学号为18的学生留下进行交流,这里运用的是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
14.已知f(x)是定义在R上的奇函数,且当x<0时,$f(x)=2_{\;}^x$,则f(log23)的值为( )
| A. | -3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
18.现有A,B,C三种产品需要检测,产品数量如下表:
已知采用分层抽样的方法从以上产品中共抽取了7件.
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
| 产品 | A | B | C |
| 数量 | 800 | 800 | 1200 |
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
15.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)在区间(0,π)上存在唯一一个x0∈(0,π),使得f(x0)=1,则
( )
( )
| A. | ω的最小值为$\frac{1}{3}$ | B. | ω的最小值为$\frac{1}{2}$ | C. | ω的最大值为$\frac{11}{6}$ | D. | ω的最大值为$\frac{13}{6}$ |
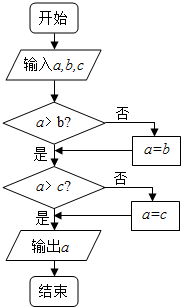 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )