题目内容
10.已知圆C过点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.(1)求圆C的方程;
(2)设Q为圆心C上的一个动点,求$\overrightarrow{CQ}$•$\overrightarrow{MQ}$的最小值;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
分析 (1)利用对称性,求出圆心坐标,即可求出圆C的方程;
(2)利用向量的数量积公式,结合三角函数知识,即可得出结论;
(3)由已知可得直线PA和直线PB的斜率存在,且互为相反数,设PA:y-$\frac{\sqrt{2}}{2}$=k(x-$\frac{\sqrt{2}}{2}$),PB:y-$\frac{\sqrt{2}}{2}$=-k(x-$\frac{\sqrt{2}}{2}$),求出A,B坐标后,代入斜率公式,判断直线OP和AB斜率是否相等,即可得到答案.
解答 (1)解:由题意可得点C和点M(-2,-2)关于直线x+y+2=0对称,
且圆C和圆M的半径相等,都等于r.
设C(m,n),由$\frac{m+2}{n+2}$•(-1)=-1,且$\frac{m-2}{2}$+$\frac{n-2}{2}$+2=0,
求得m=n=0,
故圆C的方程为x2+y2=r2.
再把点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),代入圆C的方程,求得r=1,
故圆的方程为x2+y2=1.
(2)解:设Q(x,y),则x2+y2=1,
$\overrightarrow{CQ}$•$\overrightarrow{MQ}$=(x,y)•(x+2,y+2)=x2+y2+2x+2y=2x+2y+1,
令x=cosθ,y=sinθ,
∴$\overrightarrow{CQ}$•$\overrightarrow{MQ}$=2cosθ+2sinθ+1=2$\sqrt{2}$sin(θ+$\frac{π}{4}$)+1,
∴θ+$\frac{π}{4}$=2kπ-$\frac{π}{2}$时,sin(θ+$\frac{π}{4}$)的最小值为-1,
∴$\overrightarrow{CQ}$•$\overrightarrow{MQ}$的最小值为-2$\sqrt{2}$+1;
(3)证明:过点P作两条相异直线分别与圆C相交于A,B,
且直线PA和直线PB的倾斜角互补,O为坐标原点,
则得直线OP和AB平行,
理由如下:由题意知,直线PA和直线PB的斜率存在,且互为相反数,
故可设PA:y-$\frac{\sqrt{2}}{2}$=k(x-$\frac{\sqrt{2}}{2}$),PB:y-$\frac{\sqrt{2}}{2}$=-k(x-$\frac{\sqrt{2}}{2}$).
由PA与圆方程联立,得(1+k2)x2+$\sqrt{2}$k(1-k)x+$\frac{1}{2}$(1-k)2-1=0,
因为P的横坐标x=$\frac{\sqrt{2}}{2}$一定是该方程的解,故可得xA=$\frac{\sqrt{2}}{2}$•$\frac{{k}^{2}-2k-1}{1+{k}^{2}}$.
同理,所以xB=$\frac{\sqrt{2}}{2}$•$\frac{{k}^{2}+2k-1}{1+{k}^{2}}$.
由于AB的斜率kAB=$\frac{{y}_{B}-{y}_{A}}{{x}_{B}-{x}_{A}}$=$\frac{\sqrt{2}k-k({x}_{B}+{x}_{A})}{{x}_{B}-{x}_{A}}$=1=kOP (OP的斜率),
所以,直线AB和OP一定平行.
点评 本题考查的知识点是直线和圆的方程的应用,关于直线对称的圆的方程,其中根据已知条件求出圆C的方程是解答本题的关键,考查运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | (10,12) | B. | [10,12) | C. | (10,12] | D. | [10,12] |
| 产品 | A | B | C |
| 数量 | 800 | 800 | 1200 |
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
| A. | (1,2) | B. | (5,2) | C. | (2,5) | D. | (2.5,5) |
( )
| A. | ω的最小值为$\frac{1}{3}$ | B. | ω的最小值为$\frac{1}{2}$ | C. | ω的最大值为$\frac{11}{6}$ | D. | ω的最大值为$\frac{13}{6}$ |
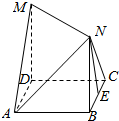 如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点