题目内容
8.由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x-y+2≥0}\end{array}\right.$确定的平面区域记为Ω1,不等式组$\left\{\begin{array}{l}{x+y-1≤0}\\{x+y+2≥0}\end{array}\right.$确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
分析 作出不等式组对应的平面区域,求出对应的面积,利用几何槪型的概率公式即可得到结论.
解答 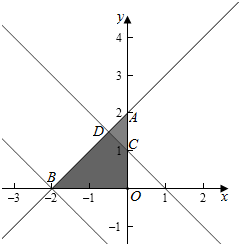 解:平面区域Ω1,为三角形AOB,面积为$\frac{1}{2}×2×2=2$,
解:平面区域Ω1,为三角形AOB,面积为$\frac{1}{2}×2×2=2$,
平面区域Ω2,为△AOB内的四边形BDCO,
其中C(0,1),
由$\left\{\begin{array}{l}{y-x-2=0}\\{x+y=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,即D($-\frac{1}{2}$,$\frac{3}{2}$),
则三角形ACD的面积S=$\frac{1}{2}×1×\frac{1}{2}$=$\frac{1}{4}$,
则四边形BDCO的面积S=${S}_{△OAB}-{S}_{△ACD}=2-\frac{1}{4}=\frac{7}{4}$,
则在Ω1中随机取一点,则该点恰好在Ω2内的概率为$\frac{\frac{7}{4}}{2}=\frac{7}{8}$,
故选:D.
点评 本题主要考查几何槪型的概率计算,利用线性规划的知识求出对应的区域和面积是解决本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.定义$\frac{n}{{p}_{1}+{p}_{2}+…+{p}_{n}}$为n个正数p1,p2,…,pn的“均倒数”,若已知数列{an},的前n项的“均倒数”为$\frac{1}{5n}$,又bn=$\frac{{a}_{n}}{5}$,则$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{10}{b}_{11}}$=( )
| A. | $\frac{8}{17}$ | B. | $\frac{9}{19}$ | C. | $\frac{10}{21}$ | D. | $\frac{11}{23}$ |
20.如图是运算2+4+6+8+10的程序框图,则其中实数m的取值范围是( )
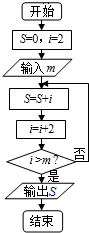

| A. | (10,12) | B. | [10,12) | C. | (10,12] | D. | [10,12] |
17.一个年级有20个班,每个班同学从1~50排学号,为了交流学习经验,要求每班学号为18的学生留下进行交流,这里运用的是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
18.现有A,B,C三种产品需要检测,产品数量如下表:
已知采用分层抽样的方法从以上产品中共抽取了7件.
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
| 产品 | A | B | C |
| 数量 | 800 | 800 | 1200 |
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
