题目内容
7.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为1.分析 根据数量积的几何意义可知,在$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影方向上的投影为|$\overrightarrow{a}$|与向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值的乘积,即可求得答案.
解答 解:根据数量积的几何意义可知,在$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影方向上的投影为|$\overrightarrow{a}$|与向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值的乘积,
∴$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为|$\overrightarrow{a}$|•cos$\frac{π}{3}$=2×$\frac{1}{2}$=1,
∴$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为1.
故答案为:1.
点评 本题考查向量投影的定义,熟练记准投影的定义是解决问题的关键,属基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
17.一个年级有20个班,每个班同学从1~50排学号,为了交流学习经验,要求每班学号为18的学生留下进行交流,这里运用的是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
18.现有A,B,C三种产品需要检测,产品数量如下表:
已知采用分层抽样的方法从以上产品中共抽取了7件.
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
| 产品 | A | B | C |
| 数量 | 800 | 800 | 1200 |
(1)求分别抽取的三种产品件数;
(2)已知被抽取的A,B,C三种产品中,一等品分别有1件、2件、2件,现再从已抽取的A,B,C三件产品中各抽取1件,求3件产品都是一等品的概率.
15.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)在区间(0,π)上存在唯一一个x0∈(0,π),使得f(x0)=1,则
( )
( )
| A. | ω的最小值为$\frac{1}{3}$ | B. | ω的最小值为$\frac{1}{2}$ | C. | ω的最大值为$\frac{11}{6}$ | D. | ω的最大值为$\frac{13}{6}$ |
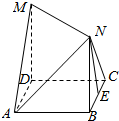 如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点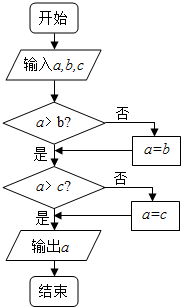 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )
已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=log5x+x的零点依次为x1、x2、x3,若在如图所示的算法中,另a=x1,b=x2,c=x3,则输出的结果是( )