题目内容
8.已知直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数,α=$\frac{π}{4}$),以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相同的长度单位,建立极坐标系.曲线C的极坐标方程为ρsin2θ=4cosθ.(1)求曲线C的直角坐标方程:
(2)设直线1与曲线C相交于A、B两点.求|AB|.
分析 (1)利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出;
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$,代入抛物线方程,可得根与系数的关系,利用|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$,即可得出.
解答 解:(1)曲线C的极坐标方程为ρsin2θ=4cosθ,即ρ2sin2θ=4ρcosθ,可得直角坐标方程:y2=4x.
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$,代入抛物线方程可得:${t}^{2}-4\sqrt{2}t$-8=0.
∴t1+t2=4$\sqrt{2}$,t1t2=-8,
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{(4\sqrt{2})^{2}-4×(-8)}$=8.
点评 本题考查了极坐标化为直角坐标、直线的参数方程的应用、直线与抛物线相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知$tanθ=\frac{3}{4}$,那么$tan(θ+\frac{π}{4})$等于( )
| A. | -7 | B. | $-\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
3.在△OAB中,O为直角坐标系的原点,A,B的坐标分别为A(3,4),B(-2,y),向量$\overrightarrow{AB}$与x轴平行,则向量$\overrightarrow{OA}$与$\overrightarrow{AB}$所成的余弦值是( )
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
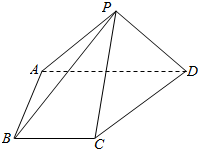 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2. 如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)
如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是$\frac{8π}{3}$.(结果保留π)