题目内容
已知点P是抛物线y2=4x上的点，设点P到抛物线的准线的距离为d1，到圆（x+3）2+（y-3）2=1上的动点Q距离为d2，则d1+d2的最小值是 ．
考点：抛物线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：由抛物线定义知：P到准线距离等于P到焦点A的距离，连结圆心B与A，交圆于C，AB交抛物线的点即为使d1+d2最小时P的位置．由此能求出结果．
解答：
解：∵点P是抛物线y2=4x上的点，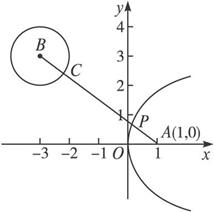
点P到抛物线的准线的距离为d1，
P到圆（x+3）2+（y-3）2=1上的动点Q距离为d2，
由抛物线定义知：P到准线距离等于P到焦点A的距离，
∴如图，连结圆心B与A，交圆于C，
AB交抛物线的点即为使d1+d2最小时P的位置．
∴（d1+d2）min=|AC|，
∵B（-3，3），A（1，0），
∴|AB|=
=5．|BC|=1．
∴|AC|=5-1=4．
故答案为：4．
点P到抛物线的准线的距离为d1，
P到圆（x+3）2+（y-3）2=1上的动点Q距离为d2，
由抛物线定义知：P到准线距离等于P到焦点A的距离，
∴如图，连结圆心B与A，交圆于C，
AB交抛物线的点即为使d1+d2最小时P的位置．
∴（d1+d2）min=|AC|，
∵B（-3，3），A（1，0），
∴|AB|=
| (-3-1)2+33 |
∴|AC|=5-1=4．
故答案为：4．
点评：本题考查与抛物线有关的两条线段和的最小值的求法，是中档题，解题时要熟练掌握抛物线性质．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
在直角坐标系xOy中，曲线C的参数方程为
（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立极坐标系．直线l的极坐标方程为ρcosθ-ρsinθ+1=0．则l与C的交点直角坐标为 ．
|
设a∈R，若对任意的n∈N*时，不等式(an-20)ln(
)≥0恒成立，则a的取值范围是（ ）
| n |
| a |
| A、（-∞，5] |
| B、[4，5] |
| C、（4，5） |
| D、[1，5] |